Bryły Obrotowe Sprawdzian Matematyka Wokół Nas 3

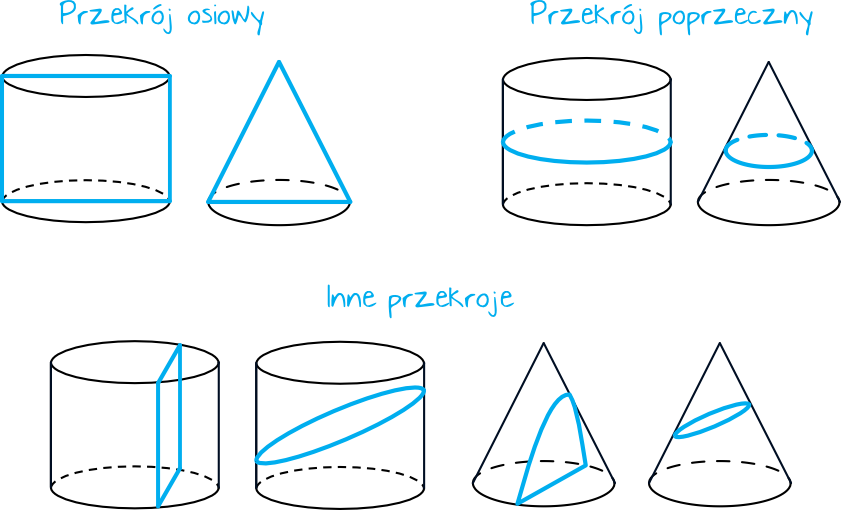
Bryły obrotowe to figury przestrzenne, które powstają przez obracanie płaskiej figury wokół prostej, zwanej osią obrotu. Wyobraź sobie, że masz płaski kształt i przyklejasz go do patyka. Kręcąc patykiem, kształt "zamiata" przestrzeń, tworząc bryłę.
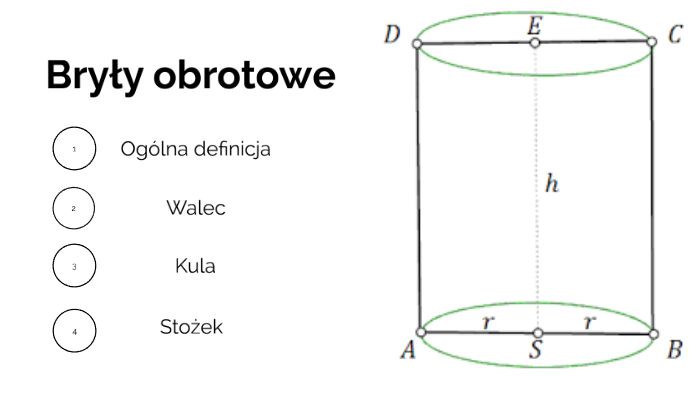
Walec
Najprostszym przykładem jest walec. Powstaje, gdy obracamy prostokąt wokół jednego z jego boków. Ten bok staje się osią obrotu. Wyobraź sobie puszkę. To jest walec! Ma dwie podstawy (koła) i powierzchnię boczną.
Wzór na objętość walca: V = πr2h, gdzie:
- V to objętość
- π (pi) to w przybliżeniu 3.14
- r to promień podstawy (koła)
- h to wysokość walca
Wzór na pole powierzchni walca: P = 2πr2 + 2πrh, gdzie:
- P to pole powierzchni
- π (pi) to w przybliżeniu 3.14
- r to promień podstawy (koła)
- h to wysokość walca
Stożek
Stożek powstaje, gdy obracamy trójkąt prostokątny wokół jednej z jego przyprostokątnych (boków przylegających do kąta prostego). Przyprostokątna staje się osią obrotu. Pomyśl o rożku do lodów. To jest stożek! Ma jedną podstawę (koło) i powierzchnię boczną.
Wzór na objętość stożka: V = (1/3)πr2h, gdzie:
- V to objętość
- π (pi) to w przybliżeniu 3.14
- r to promień podstawy (koła)
- h to wysokość stożka
Wzór na pole powierzchni stożka: P = πr2 + πrl, gdzie:
- P to pole powierzchni
- π (pi) to w przybliżeniu 3.14
- r to promień podstawy (koła)
- l to długość tworzącej stożka (od wierzchołka do brzegu podstawy)
Kula
Kula powstaje, gdy obracamy koło wokół jego średnicy. Średnica staje się osią obrotu. Wyobraź sobie piłkę. To jest kula! Nie ma podstaw ani powierzchni bocznej.
Wzór na objętość kuli: V = (4/3)πr3, gdzie:
- V to objętość
- π (pi) to w przybliżeniu 3.14
- r to promień kuli
Wzór na pole powierzchni kuli: P = 4πr2, gdzie:
- P to pole powierzchni
- π (pi) to w przybliżeniu 3.14
- r to promień kuli
Rozumienie brył obrotowych jest ważne w matematyce i fizyce. Pomaga w obliczaniu objętości i powierzchni różnych przedmiotów wokół nas. Zapamiętaj, że wszystko sprowadza się do obracania płaskich figur!