Dodawanie Ułamków Zwykłych O Różnych Mianownikach

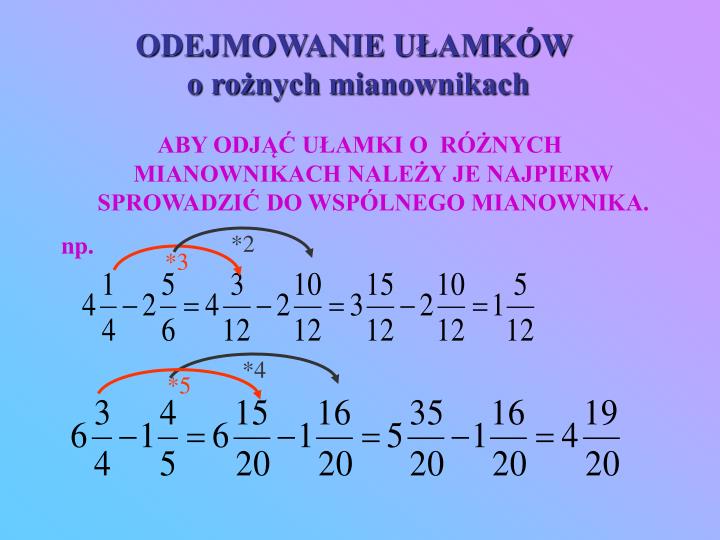
Dodawanie ułamków zwykłych o różnych mianownikach to proces łączenia dwóch lub więcej ułamków, które mają różne liczby w mianownikach (dolnej części ułamka). Zanim będziemy mogli je dodać, musimy doprowadzić je do wspólnego mianownika. To fundamentalna umiejętność w matematyce, przydatna np. przy obliczaniu proporcji w przepisach kulinarnych, dzieleniu budżetu, czy analizie danych.

Jak to zrobić? Krok po kroku:

• Krok 1: Znajdź Najmniejszą Wspólną Wielokrotność (NWW) mianowników. NWW to najmniejsza liczba, która jest podzielna przez oba mianowniki. To kluczowy krok!
• Krok 2: Rozszerz ułamki. Pomnóż licznik (górną część ułamka) i mianownik każdego ułamka przez taką liczbę, aby mianownik stał się równy NWW. Pamiętaj, że mnożysz licznik i mianownik przez tę samą liczbę, więc wartość ułamka się nie zmienia.
• Krok 3: Dodaj liczniki. Teraz, gdy ułamki mają ten sam mianownik, możesz dodać ich liczniki. Mianownik pozostaje bez zmian.
• Krok 4: Uprość wynik. Jeśli to możliwe, uprość ułamek wynikowy. Podziel licznik i mianownik przez ich największy wspólny dzielnik (NWD).

Przykłady:

Przykład 1: Dodaj 1/2 + 1/3

• Krok 1: NWW dla 2 i 3 to 6.
• Krok 2: Rozszerzamy ułamki:
  • 1/2 = (1 * 3) / (2 * 3) = 3/6
  • 1/3 = (1 * 2) / (3 * 2) = 2/6
• Krok 3: Dodajemy liczniki: 3/6 + 2/6 = 5/6
• Krok 4: Ułamek 5/6 jest już w postaci nieskracalnej.

Przykład 2: Dodaj 1/4 + 2/5

• Krok 1: NWW dla 4 i 5 to 20.
• Krok 2: Rozszerzamy ułamki:
  • 1/4 = (1 * 5) / (4 * 5) = 5/20
  • 2/5 = (2 * 4) / (5 * 4) = 8/20
• Krok 3: Dodajemy liczniki: 5/20 + 8/20 = 13/20
• Krok 4: Ułamek 13/20 jest już w postaci nieskracalnej.

Pamiętaj, praktyka czyni mistrza! Im więcej przykładów rozwiążesz, tym łatwiej będzie Ci dodawać ułamki o różnych mianownikach. Zrozumienie koncepcji NWW jest tutaj fundamentalne. Powodzenia!