Kola I Okregi Klasa 6
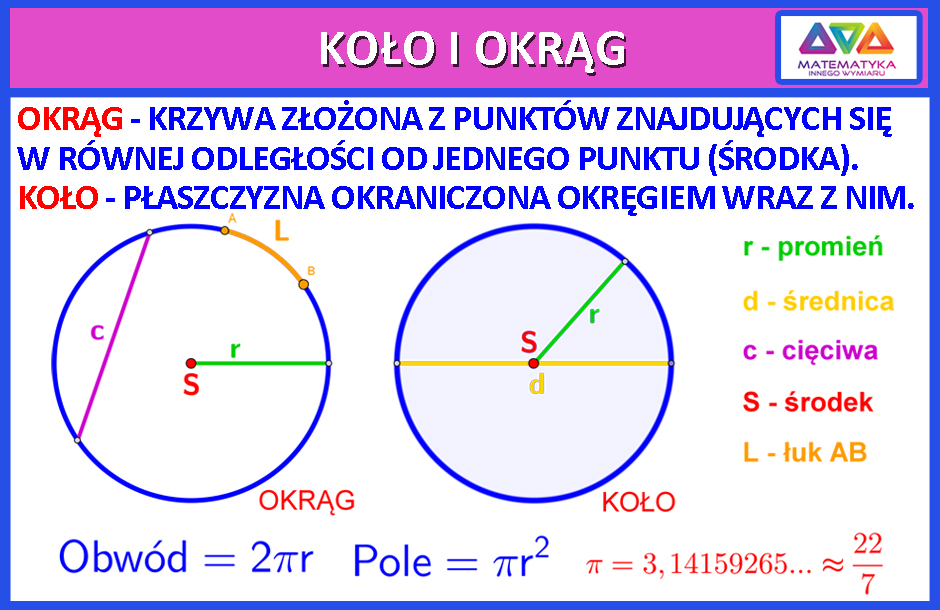
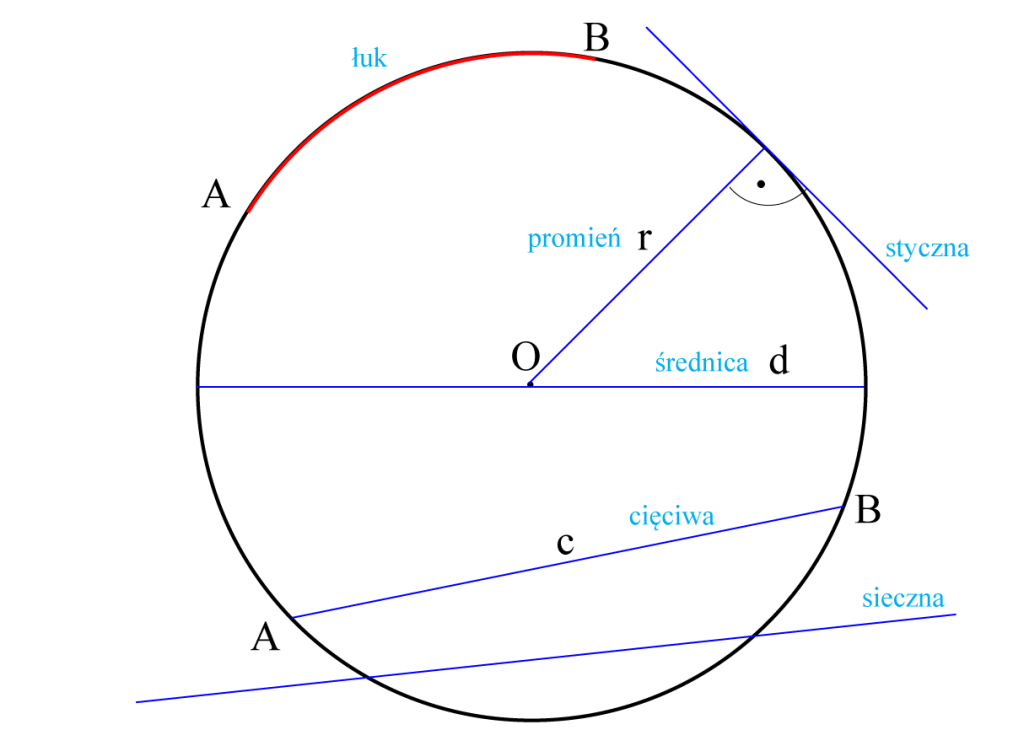
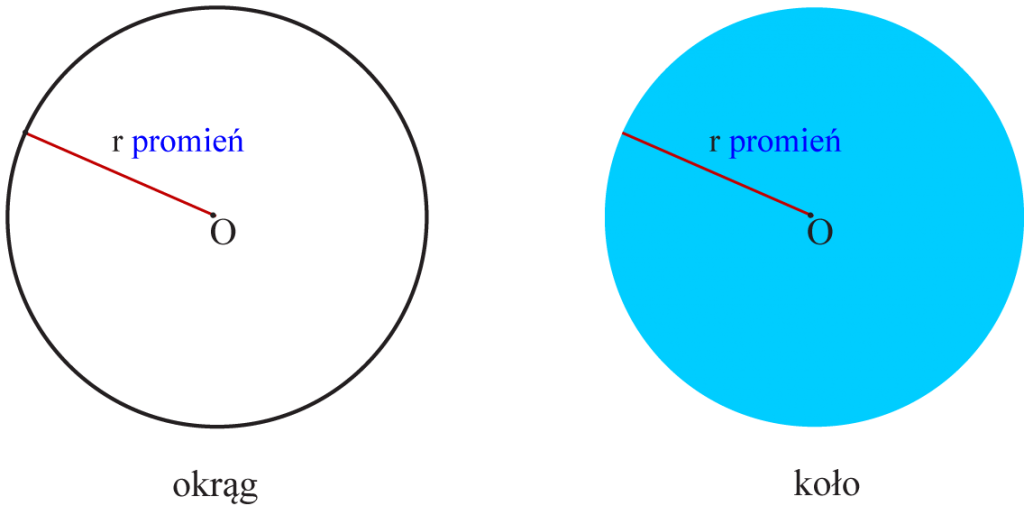
Koło to zbiór wszystkich punktów na płaszczyźnie, których odległość od jednego, ustalonego punktu (zwanego środkiem koła) jest mniejsza lub równa pewnej odległości (zwanej promieniem koła). Okrąg natomiast, to tylko brzeg koła, czyli zbiór punktów w równej odległości od środka.
Aby zrozumieć różnicę, pomyśl o pizzy. Cała pizza, włącznie z ciastem i sosem w środku, to koło. A samo ciasto, które jest na obwodzie pizzy, to okrąg.
Krok po kroku:
- Znajdź środek koła (S). To centralny punkt, od którego mierzona jest odległość.
- Zdefiniuj promień (r). To odległość od środka koła do dowolnego punktu na okręgu. Na przykład, jeśli promień wynosi 5 cm, to każdy punkt na okręgu jest oddalony od środka o 5 cm.
- Zaznacz dowolny punkt (A) na płaszczyźnie.
- Zmierz odległość od punktu A do środka koła (S).
- Jeśli odległość AS jest mniejsza lub równa promieniowi (r), punkt A należy do koła. Jeśli jest równa promieniowi, punkt A leży na okręgu. Jeśli jest większa, punkt A leży poza kołem. Na przykład: jeśli promień wynosi 5cm, a odległość AS wynosi 3cm, to punkt A należy do koła. Jeśli AS wynosi 5 cm, punkt A leży na okręgu. Jeśli AS wynosi 7cm, punkt A leży poza kołem.
Dzięki temu rozróżnieniu możemy dokładnie opisywać obiekty i kształty w naszym otoczeniu. Na przykład, możemy obliczyć pole powierzchni koła (πr²) lub długość okręgu (2πr). Znajomość tych pojęć jest kluczowa w geometrii, fizyce i wielu innych dziedzinach.
Praktyczne zastosowanie: Wyobraź sobie projektowanie kół zębatych. Musisz dokładnie znać promień i średnicę każdego koła, aby mechanizm działał prawidłowo. Kolejny przykład to projektowanie monet – średnica (czyli dwukrotność promienia) musi być precyzyjna, aby monety pasowały do automatów.