Liczby Naturalne Całkowite Wymierne I Niewymierne

Witaj! Dzisiaj zgłębimy fascynujący świat liczb. Poznamy różne rodzaje liczb, które spotykasz na co dzień. Zrozumiemy, czym są liczby naturalne, całkowite, wymierne i niewymierne.

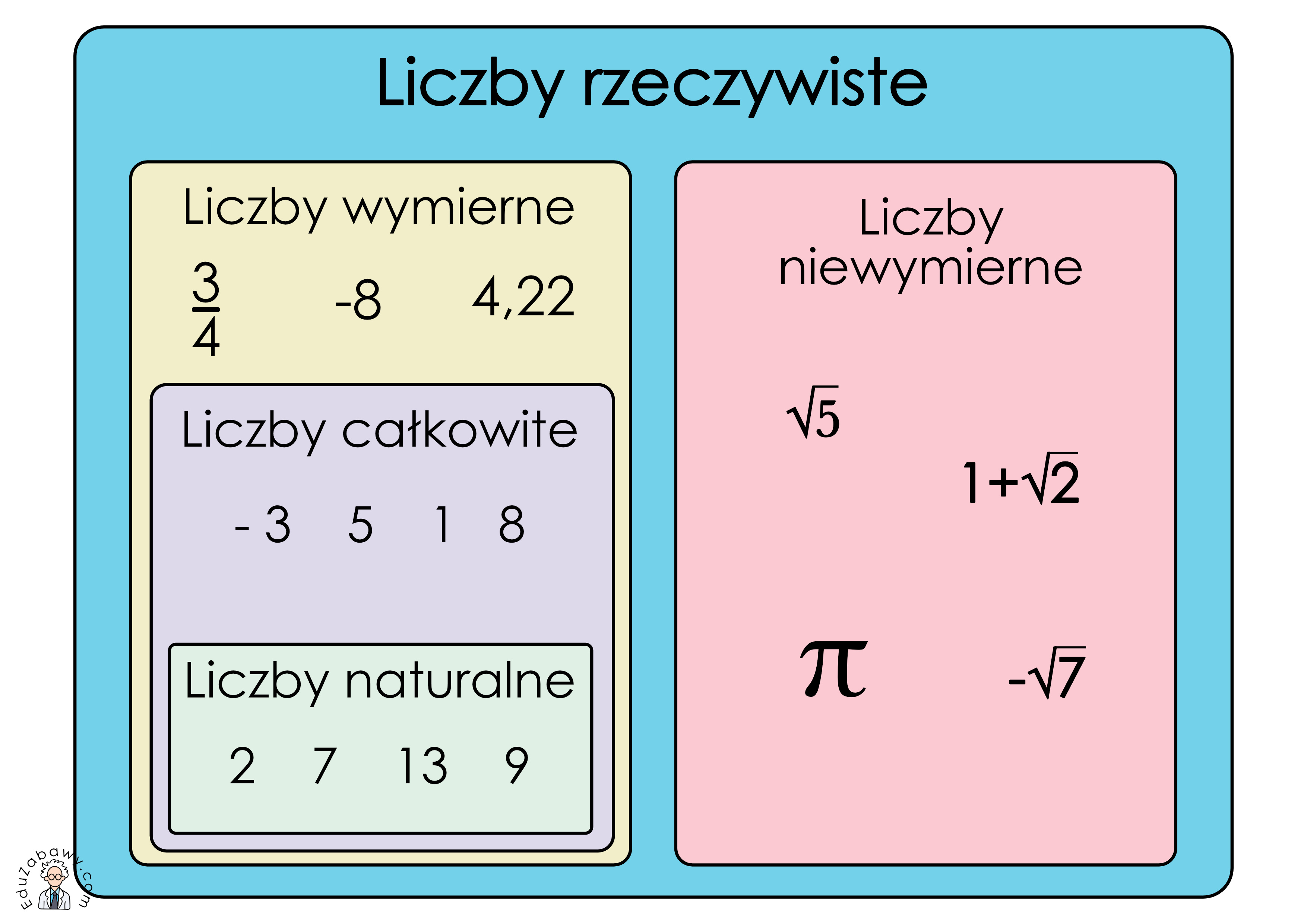
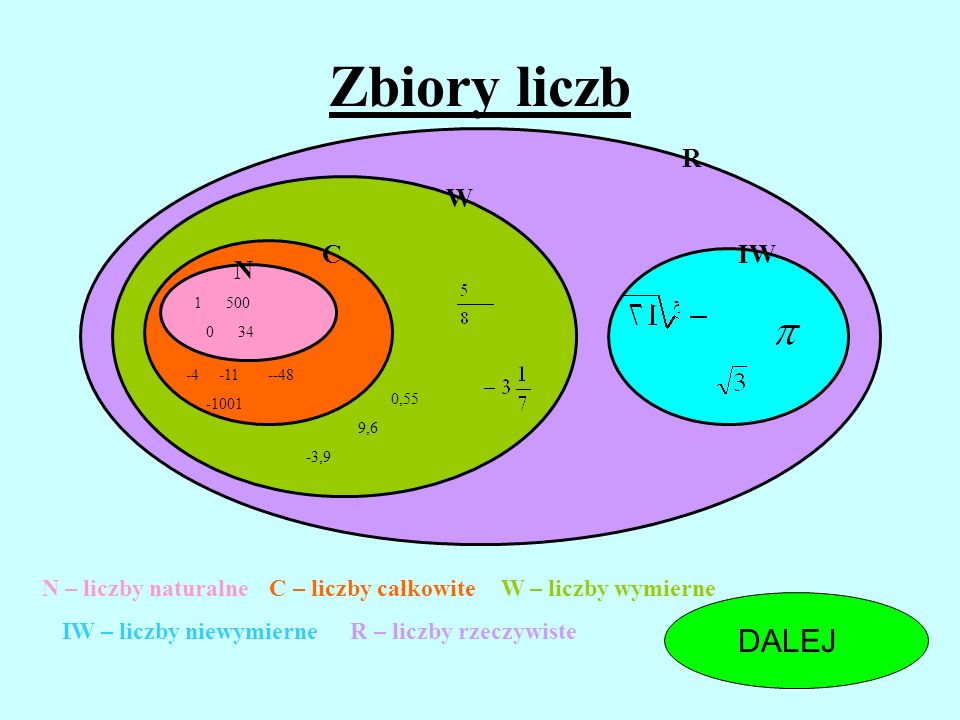
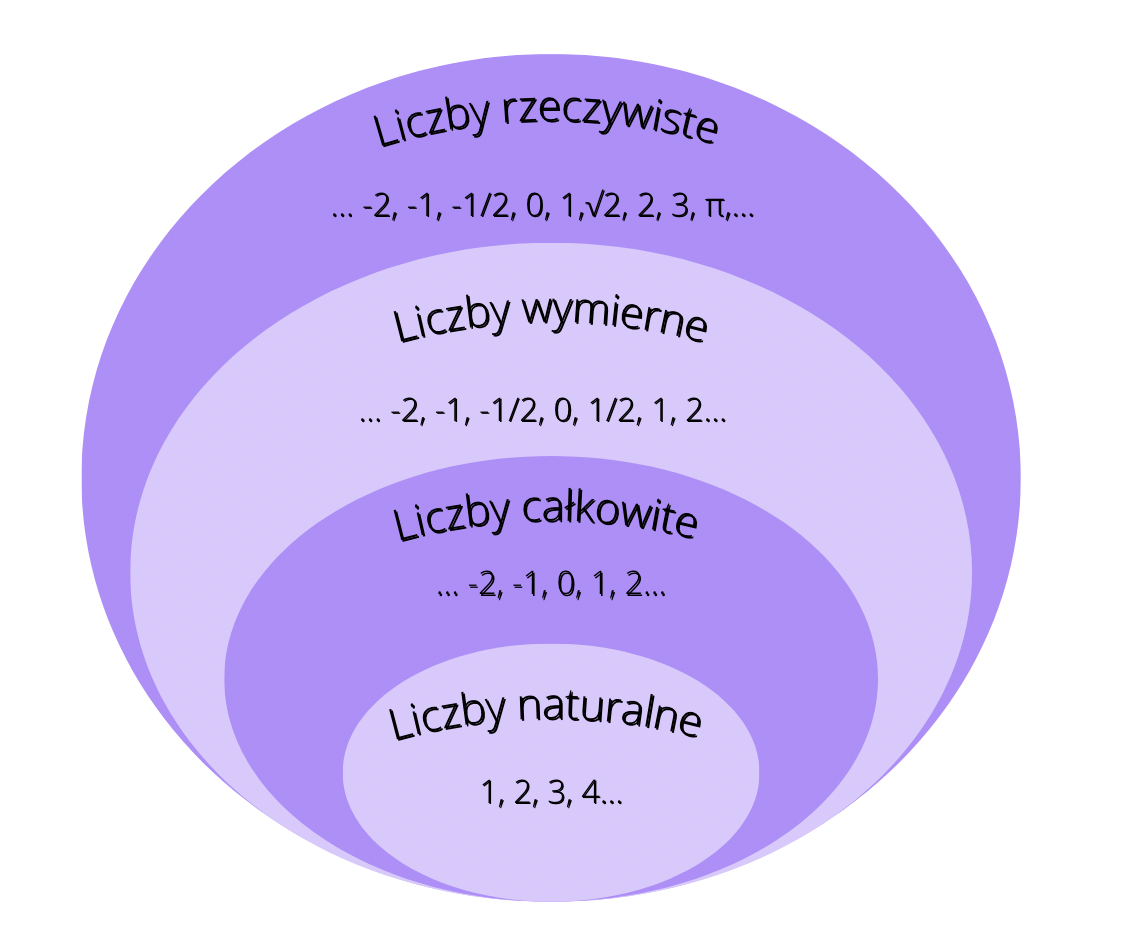
Liczby Naturalne

Zacznijmy od początku, od liczb, których używamy do liczenia. Są to liczby naturalne. Możemy ich używać do policzenia jabłek w koszyku, książek na półce, czy palców u rąk. Liczby naturalne to: 1, 2, 3, 4, 5 i tak dalej, aż do nieskończoności. Zero (0) czasami jest zaliczane do liczb naturalnych, a czasami nie – zależy to od konwencji.

Zastanów się: czy możesz mieć -3 jabłka? Nie! Dlatego liczby naturalne są zawsze dodatnie i całkowite. Nie ma ułamków ani liczb ujemnych w zbiorze liczb naturalnych. Pomyśl o nich jak o podstawowych narzędziach do liczenia przedmiotów.

Liczby Całkowite

Teraz rozszerzmy nasz zbiór liczb. Wprowadzamy liczby całkowite. Liczby całkowite zawierają wszystkie liczby naturalne, zero i liczby ujemne. Przykłady liczb całkowitych: -3, -2, -1, 0, 1, 2, 3...

Możesz myśleć o liczbach ujemnych jako o długu. Jeżeli masz 0 zł, a pożyczysz 5 zł, to masz -5 zł. Termometr może pokazywać -2 stopnie Celsjusza – to też jest liczba całkowita. Liczby całkowite pozwalają nam opisywać sytuacje poniżej zera lub niedobór czegoś.

Liczby Wymierne

Kolejny krok to liczby wymierne. To liczby, które można zapisać jako ułamek, gdzie licznik i mianownik są liczbami całkowitymi, a mianownik jest różny od zera. Na przykład 1/2, 3/4, -2/5, 7/1 to liczby wymierne. Każda liczba całkowita jest też liczbą wymierną, bo np. 5 można zapisać jako 5/1.

Liczby wymierne mają rozwinięcie dziesiętne skończone (np. 1/4 = 0.25) lub nieskończone okresowe (np. 1/3 = 0.333...). Oznacza to, że po przecinku powtarza się pewien ciąg cyfr. Liczby wymierne są bardzo powszechne w życiu codziennym, np. gdy dzielisz pizzę na kawałki.

Liczby Niewymierne

Ostatnia grupa to liczby niewymierne. To liczby, których nie można zapisać w postaci ułamka zwykłego. Ich rozwinięcie dziesiętne jest nieskończone i nieokresowe. Oznacza to, że cyfry po przecinku nie powtarzają się w żaden sposób.

Najbardziej znanym przykładem jest liczba π (pi), która opisuje stosunek obwodu koła do jego średnicy. Jej wartość to w przybliżeniu 3.14159265... ale rozwinięcie dziesiętne nigdy się nie kończy i nie powtarza. Inne przykłady to pierwiastki kwadratowe z liczb, które nie są kwadratami liczb całkowitych, np. √2, √3, √5. Liczby niewymierne mogą wydawać się abstrakcyjne, ale są fundamentalne w matematyce i fizyce.

Podsumowując: zaczęliśmy od liczb naturalnych, przez całkowite i wymierne, aż do niewymiernych. Każdy zbiór zawiera w sobie poprzedni (z pewnymi wyjątkami dotyczącymi definicji zera). Mam nadzieję, że teraz świat liczb jest dla Ciebie bardziej zrozumiały!