Mnozenie I Dzielenie Poteg O Tym Samym Wykladniku
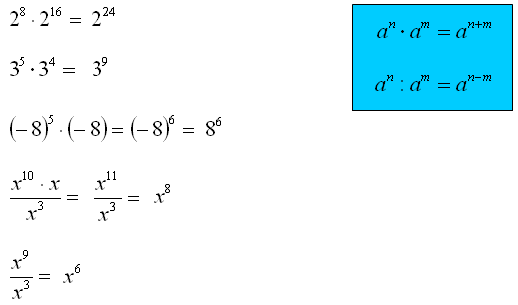
Mnożenie i dzielenie potęg o tym samym wykładniku to zasady matematyczne ułatwiające operacje na potęgach. Mówią one, że mnożąc potęgi o różnych podstawach, ale identycznym wykładniku, możemy pomnożyć podstawy i podnieść wynik do tego wykładnika. Analogicznie, dzieląc potęgi o różnych podstawach, ale tym samym wykładniku, dzielimy podstawy i podnosimy wynik do tego wykładnika.
Kluczowym aspektem jest ten sam wykładnik. Bez niego, zasady te nie mają zastosowania. Działają one zarówno dla wykładników naturalnych, jak i rzeczywistych.
Formalnie, możemy to zapisać w następujący sposób:
- Mnożenie: an * bn = (a * b)n
- Dzielenie: an / bn = (a / b)n, gdzie b ≠ 0
Spójrzmy na proste przykłady:
- 23 * 53 = (2 * 5)3 = 103 = 1000
- 62 / 32 = (6 / 3)2 = 22 = 4
Zauważmy, że kolejność działań jest tutaj uproszczona. Zamiast obliczać każdą potęgę oddzielnie, a potem mnożyć lub dzielić, możemy najpierw wykonać mnożenie lub dzielenie podstaw, a dopiero potem podnieść wynik do potęgi.
Zastosowanie tych zasad znajduje się w wielu dziedzinach, od obliczeń naukowych po inżynierię i informatykę. Upraszczają one zapis i obliczenia w problemach związanych z powierzchniami, objętościami i w wielu innych sytuacjach, gdzie operujemy na wartościach podniesionych do potęgi.




