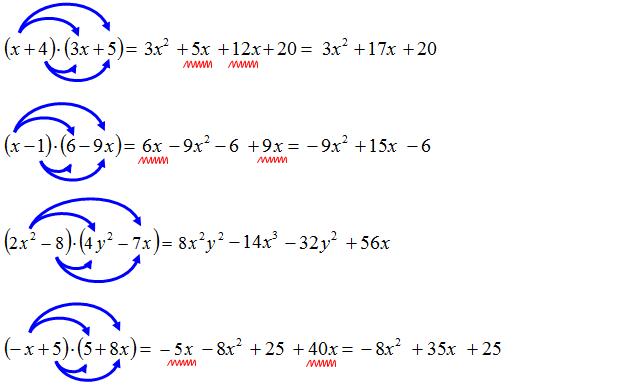Mnożenie Sum Algebraicznych Gimnazjum Sprawdzian

Mnożenie sum algebraicznych to temat, który często pojawia się na sprawdzianach w gimnazjum. Brzmi poważnie, ale spokojnie! To tylko proste mnożenie, tylko trochę bardziej rozbudowane.

Co to jest suma algebraiczna?

Najpierw przypomnijmy sobie, co to jest suma algebraiczna. To wyrażenie, w którym mamy litery (zmienne, np. x, y) połączone znakami dodawania (+) i odejmowania (-). Przykład: 2x + 3y - 5.

Na czym polega mnożenie sum algebraicznych?

Mnożenie sum algebraicznych to nic innego, jak mnożenie każdego elementu jednej sumy przez każdy element drugiej sumy. Używamy do tego zasady rozdzielności mnożenia względem dodawania i odejmowania.

Krok po kroku - jak to zrobić?

Oto, jak to zrobić krok po kroku z przykładami:

Zapisz wyrażenie. Na przykład: (a + b)(c + d)
Pomnóż pierwszy element pierwszej sumy przez każdy element drugiej sumy. Czyli: a * c + a * d
Pomnóż drugi element pierwszej sumy przez każdy element drugiej sumy. Czyli: b * c + b * d
Zapisz wszystko razem. Otrzymujemy: ac + ad + bc + bd

Przykład 1: Prosty przypadek

Obliczmy (x + 2)(x + 3).

x * x = x²
x * 3 = 3x
2 * x = 2x
2 * 3 = 6

Teraz dodajemy wszystko razem: x² + 3x + 2x + 6. Na koniec upraszczamy wyrażenie, redukując wyrazy podobne: x² + 5x + 6.

Przykład 2: Z minusem

A co, jeśli mamy minus? Obliczmy (y - 1)(y + 4).

y * y = y²
y * 4 = 4y
-1 * y = -y
-1 * 4 = -4

Dodajemy: y² + 4y - y - 4. Upraszczamy: y² + 3y - 4.

Przykład 3: Trochę trudniejszy

Spróbujmy z (2a + 1)(3a - 2).

2a * 3a = 6a²
2a * -2 = -4a
1 * 3a = 3a
1 * -2 = -2

Dodajemy: 6a² - 4a + 3a - 2. Upraszczamy: 6a² - a - 2.

Wskazówki na sprawdzian

Uważaj na znaki! Minusy potrafią narobić bałaganu.
Upraszczaj wyrażenia. Dodaj wyrazy podobne (np. 3x i 2x).
Sprawdzaj swoje obliczenia. Lepiej dwa razy policzyć, niż stracić punkty.
Pamiętaj o wzorach skróconego mnożenia. Czasami można je wykorzystać, żeby szybciej rozwiązać zadanie (np. (a+b)² = a² + 2ab + b²).

Mnożenie sum algebraicznych to podstawa algebry. Ćwicz regularnie, a szybko zobaczysz, że to wcale nie jest takie trudne! Powodzenia na sprawdzianie!