Ostrosłupy I Graniastosłupy Sprawdzian Gimnazjum

Witaj! Przygotowujesz się do sprawdzianu z ostrosłupów i graniastosłupów w gimnazjum? Super! Najważniejsze to zrozumieć podstawy. Zacznijmy od definicji:
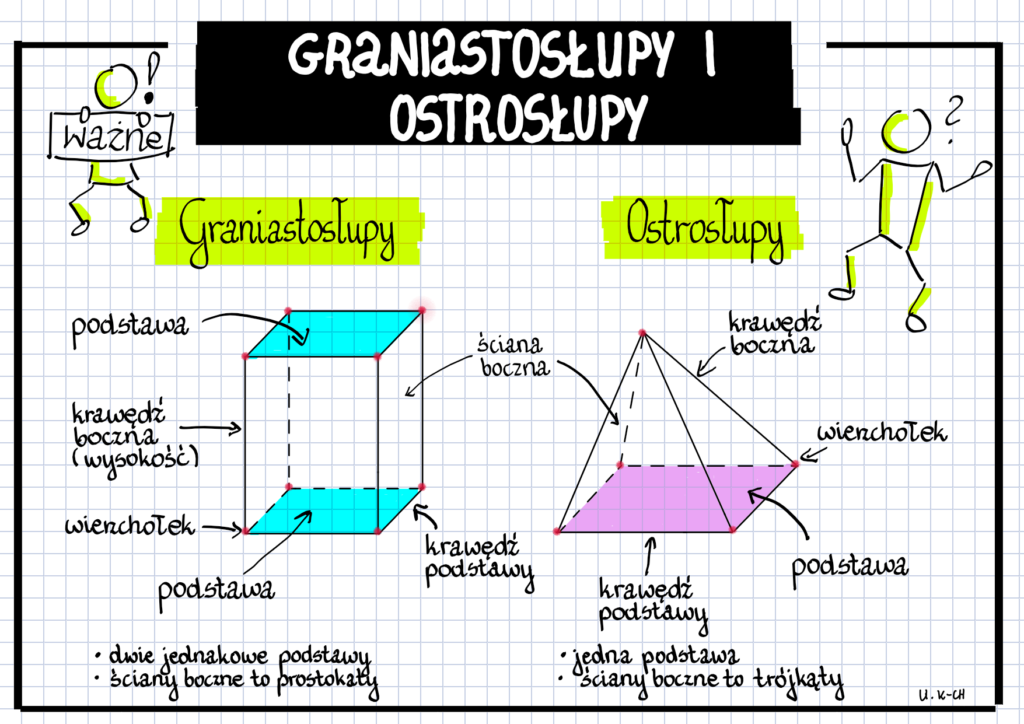
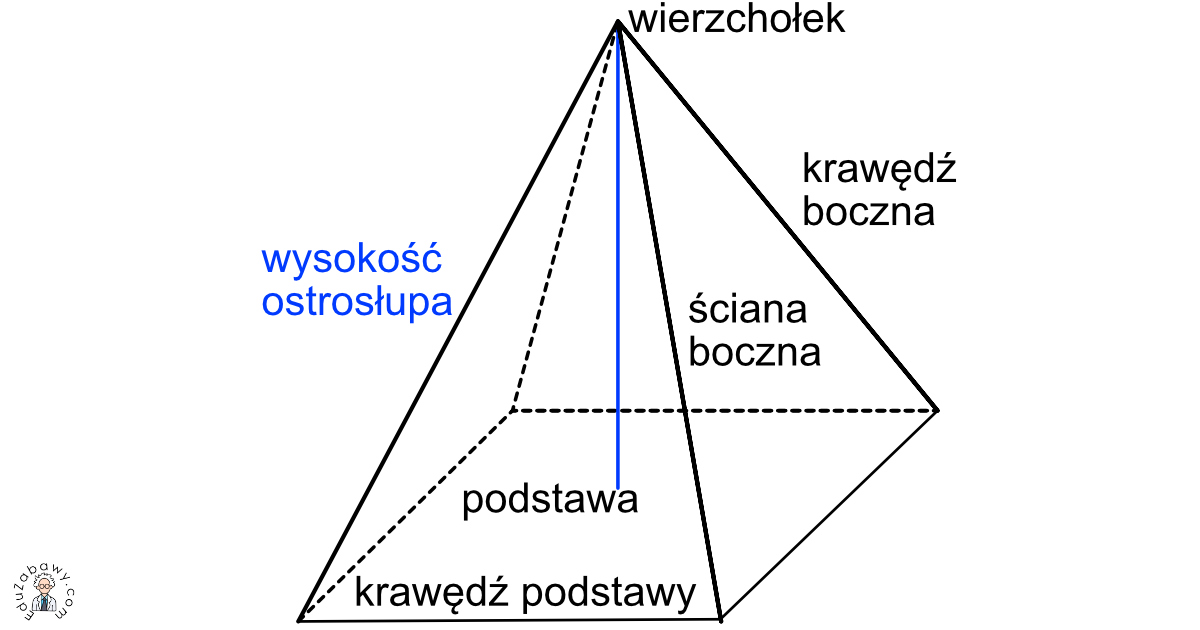
Ostrosłup to bryła, której podstawą jest wielokąt (np. trójkąt, kwadrat), a ściany boczne to trójkąty zbiegające się w jednym punkcie – wierzchołku ostrosłupa. Wyobraź sobie piramidę – to typowy ostrosłup. Z kolei graniastosłup to bryła, która ma dwie identyczne podstawy (wielokąty) leżące w równoległych płaszczyznach, połączone ścianami bocznymi będącymi równoległobokami. Pomyśl o pudełku na buty – to graniastosłup prosty.
Kluczowe elementy, które musisz znać, to:
- Podstawa: wielokąt, który definiuje bryłę.
- Wysokość: odcinek prostopadły do podstawy, łączący ją z wierzchołkiem (ostrosłup) lub drugą podstawą (graniastosłup).
- Ściany boczne: trójkąty (ostrosłup) lub równoległoboki (graniastosłup) łączące podstawę z wierzchołkiem/drugą podstawą.
Do obliczeń będziesz potrzebować wzorów na:
- Objętość ostrosłupa: V = (1/3) * Pole podstawy * Wysokość
- Objętość graniastosłupa: V = Pole podstawy * Wysokość
- Pole powierzchni całkowitej: Suma pól wszystkich ścian (podstaw i ścian bocznych).
Przykład: Oblicz objętość ostrosłupa o podstawie kwadratowej o boku 5cm i wysokości 10cm. Pole podstawy = 5cm * 5cm = 25cm². Objętość = (1/3) * 25cm² * 10cm = 83.33 cm³ (w przybliżeniu).
Gdzie to się przydaje? Architektura! Piramidy, dachy budynków, pudełka, szafy - wszystko to bazuje na tych bryłach. Rozumienie ostrosłupów i graniastosłupów pomaga zrozumieć otaczający nas świat!