Spra Fm Sprawdzian Matematyka Z Plucem 3 Funkcje
Funkcje to jeden z kluczowych tematów w matematyce. Często pojawiają się na sprawdzianach, w tym na sprawdzianach Sprawdzian Matematyka z Plusem. Zrozumienie funkcji jest niezbędne do dalszej nauki matematyki. Omówimy podstawowe pojęcia związane z funkcjami.
Czym jest funkcja?
Funkcja to relacja między dwoma zbiorami. Przyporządkowuje ona każdemu elementowi ze zbioru argumentów (zwanego dziedziną) dokładnie jeden element ze zbioru wartości (zwanego przeciwdziedziną). Można to porównać do maszyny, która na wejściu przyjmuje argument, a na wyjściu zwraca wartość. Każdy argument ma tylko jedno przypisanie.
Formalnie, funkcję oznaczamy jako f: X -> Y. X to dziedzina funkcji, a Y to przeciwdziedzina. Oznacza to, że funkcja f przekształca elementy ze zbioru X w elementy ze zbioru Y. Zapis y = f(x) oznacza, że wartość funkcji f dla argumentu x wynosi y.
Dziedzina i Zbiór Wartości
Dziedzina funkcji to zbiór wszystkich możliwych argumentów. To wszystkie liczby, które możemy "wrzucić" do naszej funkcji. Ważne jest, aby sprawdzić, czy jakieś argumenty nie są wykluczone. Na przykład, nie możemy dzielić przez zero, więc jeśli funkcja ma dzielenie, musimy wykluczyć te wartości.
Zbiór wartości funkcji to zbiór wszystkich możliwych wyników. To wszystkie liczby, które funkcja może "wypuścić" na wyjściu. Określanie zbioru wartości może być trudniejsze niż określanie dziedziny. Czasem wymaga to analizy wykresu funkcji.
Przykłady funkcji
Oto kilka przykładów funkcji:
- f(x) = 2x + 1 (funkcja liniowa)
- g(x) = x2 (funkcja kwadratowa)
- h(x) = 1/x (funkcja homograficzna)
W pierwszym przykładzie, funkcja f(x) = 2x + 1, dla argumentu x = 3, wartość funkcji wynosi f(3) = 2 * 3 + 1 = 7. Oznacza to, że funkcja przypisuje liczbie 3 liczbę 7. Podobnie, dla g(x) = x2, g(2) = 22 = 4.
Wykres funkcji
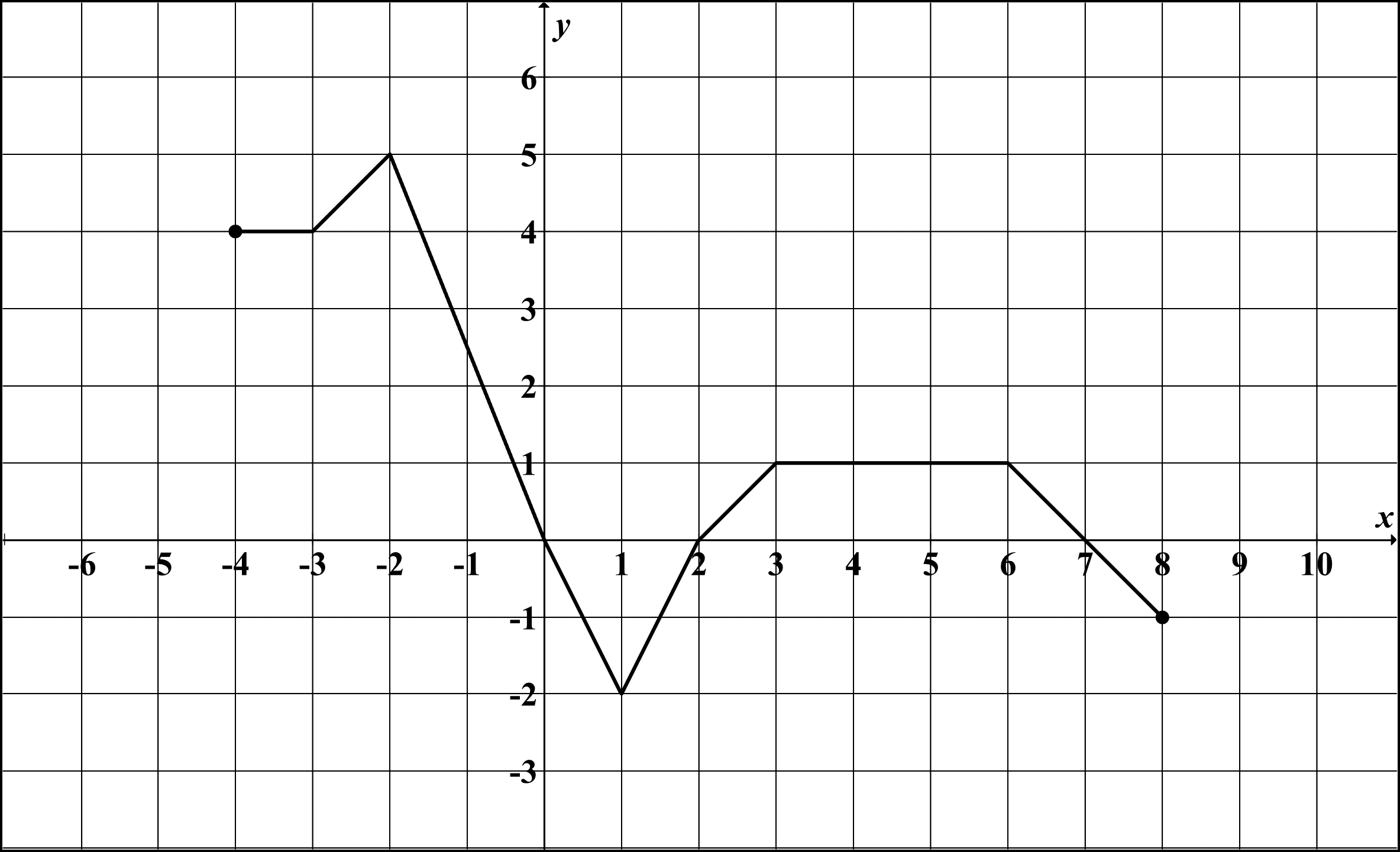
Wykres funkcji to zbiór punktów na płaszczyźnie, gdzie każdy punkt ma współrzędne (x, f(x)). Wykres pozwala wizualnie przedstawić zachowanie funkcji. Możemy zobaczyć, gdzie funkcja rośnie, maleje, ma ekstrema i jakie są jej asymptoty.
Aby narysować wykres funkcji, możemy obliczyć wartości funkcji dla kilku argumentów i zaznaczyć te punkty na płaszczyźnie. Następnie łączymy te punkty linią prostą lub krzywą, w zależności od rodzaju funkcji. Ważne jest, aby dobrać odpowiednie punkty, aby wykres był dokładny.
Praktyczne zastosowania funkcji
Funkcje mają szerokie zastosowanie w różnych dziedzinach. W fizyce opisują ruch, w ekonomii modelują popyt i podaż, w informatyce są podstawą programowania. Zrozumienie funkcji pozwala rozwiązywać problemy z różnych dziedzin. Na przykład, można użyć funkcji do obliczenia trajektorii lotu pocisku lub do przewidywania zmian cen akcji.
Nauka o funkcjach to inwestycja w przyszłość. Dobre zrozumienie tego tematu ułatwi dalszą edukację i otworzy drzwi do wielu interesujących karier. Pamiętaj, że kluczem do sukcesu jest regularna praktyka i rozwiązywanie zadań.