Sprawdzian Funkcja Liniowa 2 Lo Zadania Optwarte

Hej uczniowie! Czeka Was sprawdzian z funkcji liniowej? Nie martwcie się! Razem to ogarniemy. Zrozumienie funkcji liniowej to klucz do wielu zagadnień w matematyce i fizyce. Przygotujcie się na otwarte zadania! Przejdźmy do konkretów.

Co to jest funkcja liniowa?

Najprościej mówiąc, funkcja liniowa to taka funkcja, której wykres jest linią prostą. Wyobraźcie sobie prostą drogę. Idąc nią ze stałą prędkością, poruszacie się zgodnie z funkcją liniową. Jej ogólny wzór to: f(x) = ax + b, gdzie a i b to liczby.

f(x) to wartość funkcji dla danego x. x to argument funkcji – to, co "wrzucamy" do funkcji. a to współczynnik kierunkowy, który mówi nam, jak stroma jest prosta. b to wyraz wolny, który wskazuje, w którym miejscu prosta przecina oś Y.

Współczynnik kierunkowy (a)

Współczynnik kierunkowy, czyli a, określa nachylenie prostej. Jeśli a jest dodatnie, prosta rośnie (idzie w górę od lewej do prawej). Jeśli a jest ujemne, prosta maleje (idzie w dół od lewej do prawej). Jeżeli a wynosi 0, to prosta jest pozioma. Pomyślcie o jeździe na rowerze – im większy a, tym stromsze wzniesienie!

Wyraz wolny (b)

Wyraz wolny, czyli b, to punkt przecięcia wykresu funkcji z osią Y. Mówi nam, gdzie prosta "startuje" na osi pionowej. Na przykład, jeśli b = 2, to prosta przecina oś Y w punkcie (0, 2). Wyobraźcie sobie windę – b to numer piętra, na którym winda zaczyna jazdę.

Zadania otwarte - praktyczne przykłady

Zadania otwarte wymagają od Was więcej niż tylko podstawienia do wzoru. Często trzeba coś wymyślić, zinterpretować, narysować. Spróbujmy!

Przykład 1: Napisz równanie funkcji liniowej, która przechodzi przez punkty (1, 3) i (2, 5).

Rozwiązanie: Najpierw obliczamy a: a = (5 - 3) / (2 - 1) = 2. Następnie podstawiamy do wzoru f(x) = 2x + b. Wybieramy jeden z punktów, np. (1, 3), i podstawiamy: 3 = 2 * 1 + b. Stąd b = 1. Ostatecznie: f(x) = 2x + 1.

Przykład 2: Narysuj wykres funkcji liniowej f(x) = -x + 4. Określ, dla jakich argumentów funkcja przyjmuje wartości dodatnie.

Rozwiązanie: Wykres rysujemy, znajdując dwa punkty należące do prostej. Np. dla x = 0, f(x) = 4, a dla x = 4, f(x) = 0. Funkcja przyjmuje wartości dodatnie dla x < 4.

Kluczowe umiejętności na sprawdzian

Aby dobrze napisać sprawdzian z funkcji liniowej, musicie umieć:

• Rozpoznawać wzór funkcji liniowej.
• Obliczać współczynnik kierunkowy (a) i wyraz wolny (b).
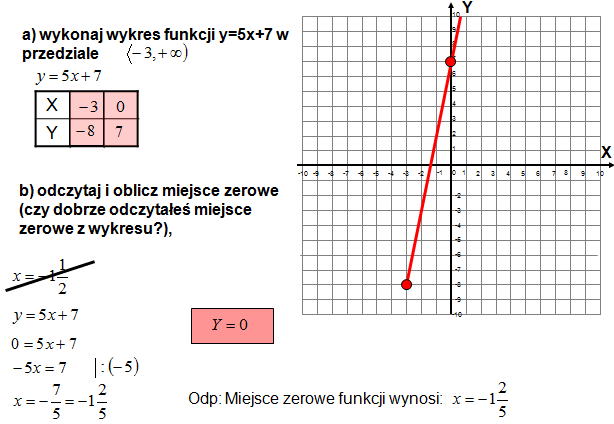
• Rysować wykres funkcji liniowej.
• Określać monotoniczność funkcji (czy rośnie, maleje, czy jest stała).
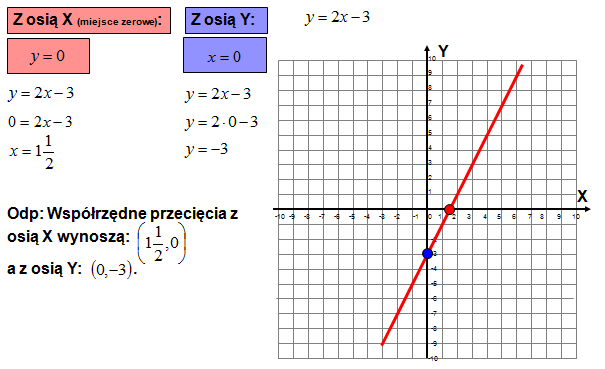
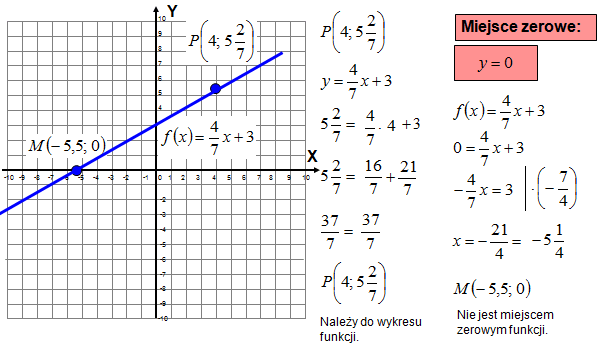
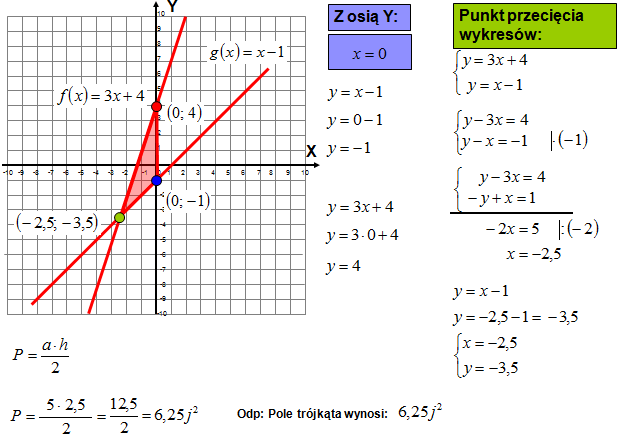
• Znajdować punkty przecięcia z osiami X i Y.
• Pisać równanie funkcji liniowej przechodzącej przez dane punkty.
• Rozwiązywać zadania tekstowe związane z funkcją liniową.

Pamiętajcie, trening czyni mistrza! Im więcej zadań rozwiążecie, tym lepiej zrozumiecie funkcję liniową. Powodzenia na sprawdzianie! Nie bójcie się zadawać pytań nauczycielowi! Każdy kiedyś zaczynał.