Sprawdzian Matematyka Klasa 6 Figury Przestrzenne

Witajcie, młodzi matematycy! Przed nami Sprawdzian Matematyka Klasa 6, a dokładniej – Figury Przestrzenne. Brzmi groźnie? Spokojnie, rozłożymy to na czynniki pierwsze. Wyobraźcie sobie, że zamieniamy się w architektów i budowniczych! Zaczynamy!

Prostopadłościan i Sześcian

Najpierw prostopadłościan. Pomyślcie o pudełku po butach, książce, albo cegle. Ma sześć ścian, a każda z nich to prostokąt. Ściany są parami równoległe i równe. To jak dwie identyczne ściany czołowe, dwie boczne i dwie na górze i na dole. Wzór na objętość prostopadłościanu? Długość razy szerokość razy wysokość (V = a * b * h). Wyobraźcie sobie wypełnianie pudełka po brzegi małymi kostkami. Objętość to właśnie liczba tych kostek!

Teraz sześcian. To specjalny rodzaj prostopadłościanu. Wszystkie jego ściany są kwadratami! Kostka do gry, kostka lodu – to idealne przykłady. Każda krawędź ma tę samą długość. Objętość sześcianu to długość krawędzi podniesiona do potęgi trzeciej (V = a³). Czyli mnożymy długość krawędzi przez siebie trzy razy.

Graniastosłup

Graniastosłup to taka figura, która ma dwie identyczne podstawy (wielokąty) i ściany boczne, które są prostokątami. Pomyślcie o pudełku czekoladek Toblerone – to graniastosłup trójkątny. Albo o namiocie – też ma trójkątną podstawę. Objentość graniastosłupa to pole podstawy razy wysokość (V = Pp * h). Najpierw liczymy pole podstawy (trójkąta, kwadratu, pięciokąta – w zależności od graniastosłupa), a potem mnożymy to przez wysokość.

Ostrosłup

Ostrosłup ma tylko jedną podstawę (wielokąt), a ściany boczne są trójkątami, które schodzą się w jednym punkcie (wierzchołku). Piramidy w Egipcie to ostrosłupy czworokątne. Dach domu może przypominać ostrosłup. Objętość ostrosłupa to jedna trzecia pola podstawy razy wysokość (V = 1/3 * Pp * h). Czyli liczymy pole podstawy, mnożymy przez wysokość, a potem dzielimy przez 3.

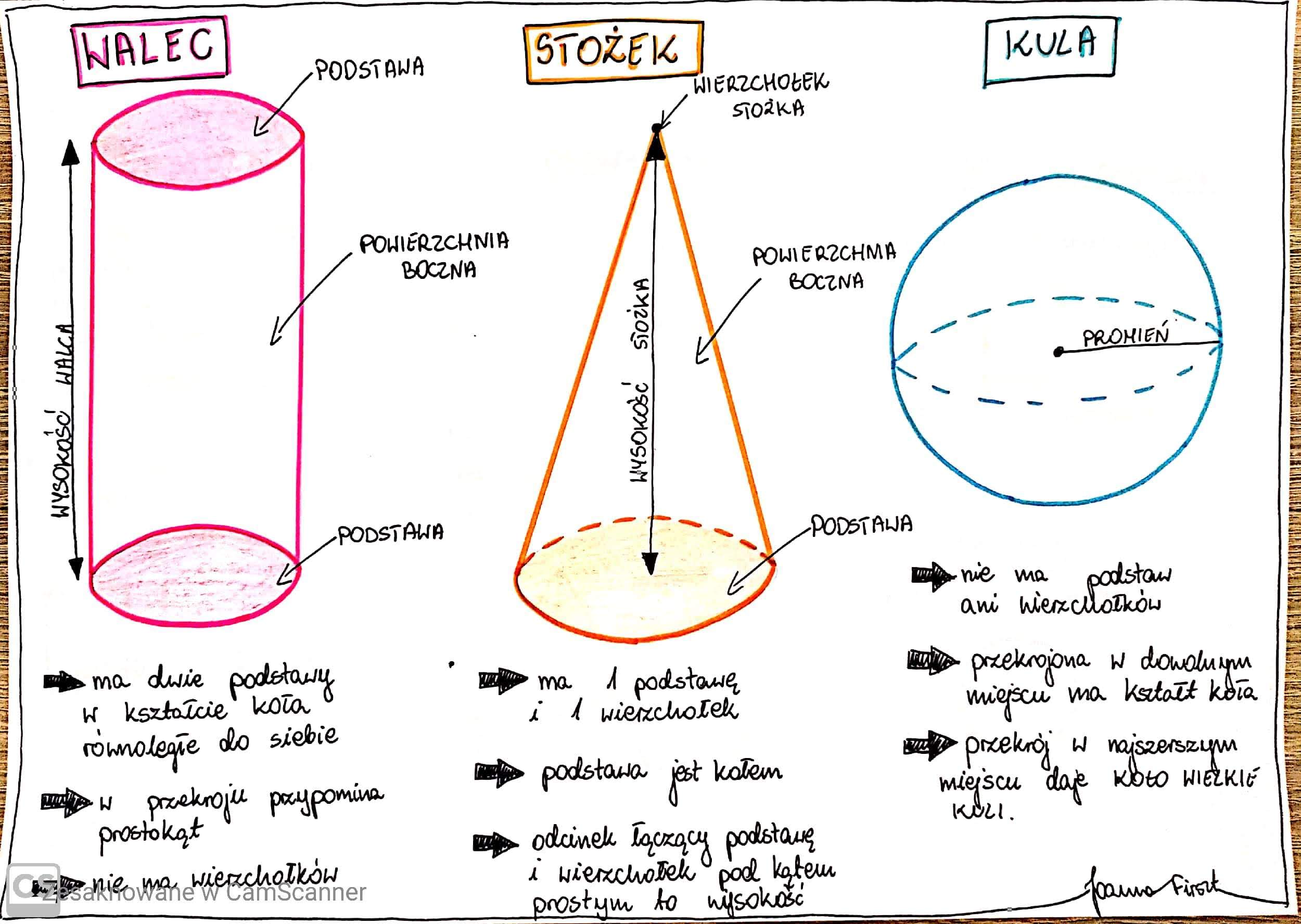
Walec

Walec to figura, która ma dwie podstawy w kształcie koła, połączone powierzchnią boczną. Konserwa, rolka papieru toaletowego, puszka z napojem – to walce. Objętość walca to pole podstawy (czyli koła) razy wysokość (V = πr²h). Pamiętacie, jak liczymy pole koła? πr² (pi razy promień do kwadratu)!

Stożek

Stożek ma jedną podstawę w kształcie koła i powierzchnię boczną, która schodzi się w jednym punkcie (wierzchołku). Lody w wafelku, lejek – to stożki. Objętość stożka to jedna trzecia pola podstawy razy wysokość (V = 1/3 * πr²h). Czyli tak jak w ostrosłupie, najpierw liczymy pole koła (πr²), mnożymy przez wysokość, a potem dzielimy przez 3.

Kula

Na koniec kula! Piłka do koszykówki, globus, kulka – to kule. Objętość kuli to cztery trzecie pi razy promień do potęgi trzeciej (V = 4/3 * πr³). Trochę skomplikowane, ale zapamiętajcie ten wzór. To jak wypełnianie piłki małymi kuleczkami, aż nie będzie już miejsca.

Pamiętajcie, figury przestrzenne to nie tylko wzory, ale przede wszystkim otaczający nas świat. Obserwujcie przedmioty dookoła, analizujcie ich kształty, a nauka pójdzie Wam jak z płatka. Powodzenia na sprawdzianie!