Sprawdzian Matematyka Ostrosłupy 2 Gimnazjum Gwo

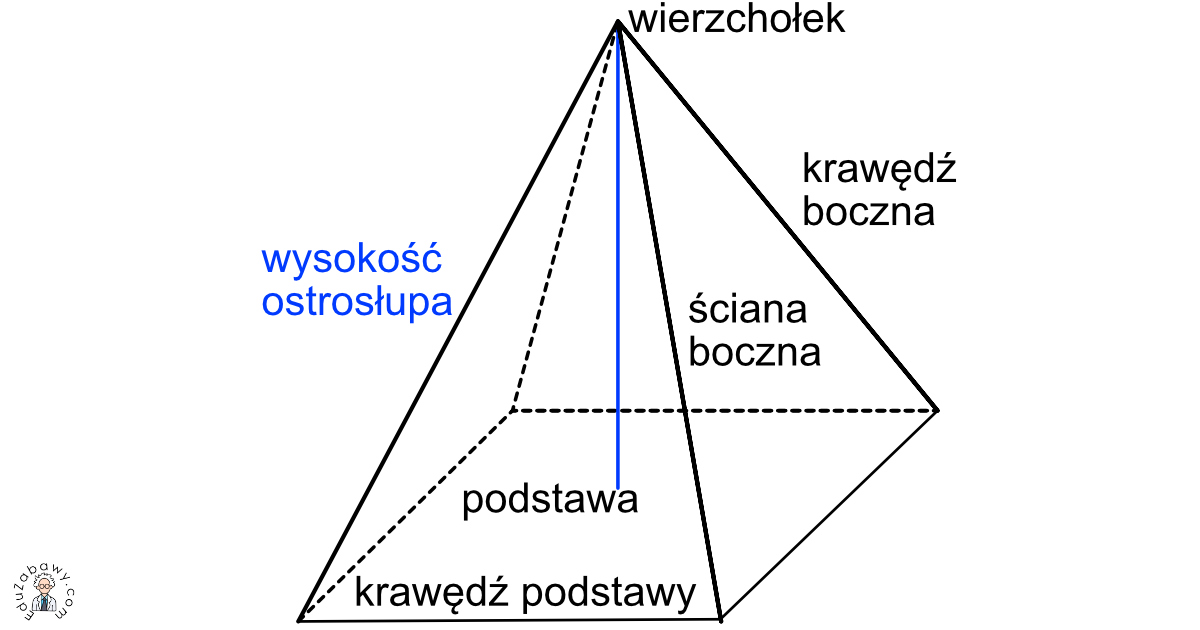
Co to jest ostrosłup? Najprościej mówiąc, to figura przestrzenna. Ma jedną podstawę (wielokąt) i ściany boczne, które są trójkątami. Wszystkie te trójkąty spotykają się w jednym punkcie – wierzchołku ostrosłupa.

Podstawa ostrosłupa: Może być dowolnym wielokątem: trójkątem, kwadratem, pięciokątem, itd. To, jaki wielokąt jest w podstawie, określa nazwę ostrosłupa. Na przykład, jeśli podstawa to kwadrat, mamy ostrosłup czworokątny. Jeśli podstawa to trójkąt, mamy ostrosłup trójkątny (znany też jako czworościan).

Ściany boczne: Są to trójkąty. Każdy bok podstawy jest podstawą trójkąta, który tworzy ścianę boczną. Ilość ścian bocznych jest zawsze równa ilości boków w podstawie. Na przykład, ostrosłup o podstawie pięciokątnej ma 5 ścian bocznych.

Wierzchołek ostrosłupa: To punkt, w którym spotykają się wszystkie ściany boczne. Jest jeden wierzchołek poza podstawą.

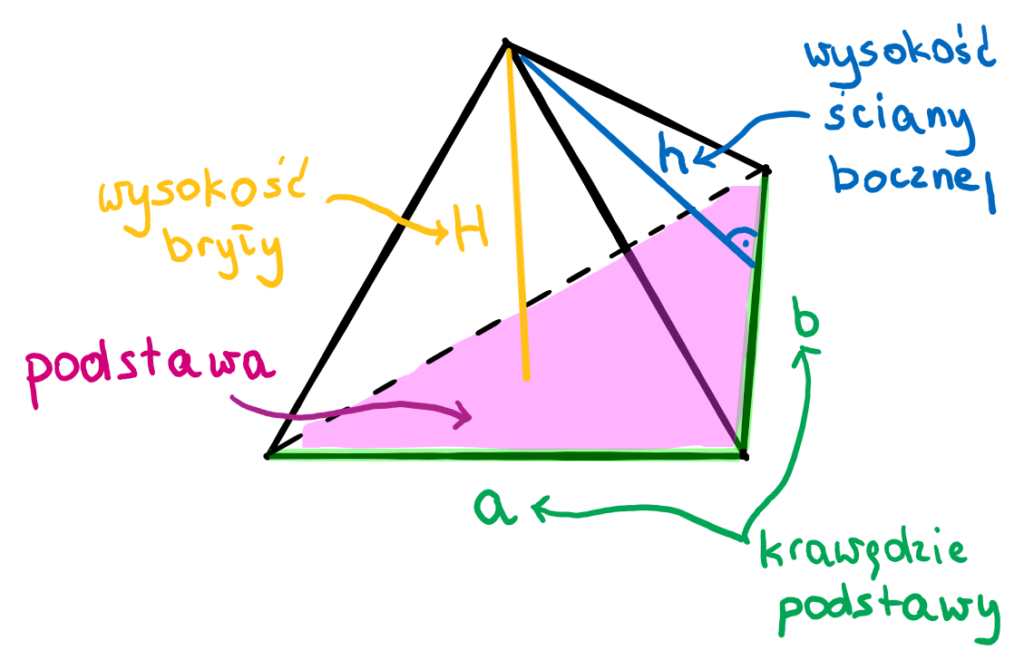
Wysokość ostrosłupa: To odcinek łączący wierzchołek ostrosłupa ze środkiem podstawy. Jest prostopadły do płaszczyzny podstawy. Wyobraź sobie, że spuszczasz linę z wierzchołka prosto w dół, aż dotknie podstawy – to jest wysokość.

Wzory, które musisz znać:

Pole powierzchni całkowitej (Pc): To suma pola podstawy (Pp) i pola powierzchni bocznej (Pb). Wzór: Pc = Pp + Pb.

Pole podstawy (Pp): Zależy od tego, jaki wielokąt jest w podstawie. Musisz znać wzory na pole trójkąta, kwadratu, prostokąta, itp.

Pole powierzchni bocznej (Pb): To suma pól wszystkich ścian bocznych (trójkątów). Każdy trójkąt ma pole liczone jako (podstawa * wysokość)/2. Podstawa to bok wielokąta w podstawie ostrosłupa, a wysokość to wysokość ściany bocznej (często nazywana też wysokością boczną).

Objętość (V): To ilość miejsca, którą zajmuje ostrosłup. Wzór: V = (1/3) * Pp * H, gdzie Pp to pole podstawy, a H to wysokość ostrosłupa.

Przykład:

Wyobraź sobie ostrosłup czworokątny prawidłowy. Oznacza to, że w podstawie ma kwadrat, a wszystkie ściany boczne są identycznymi trójkątami równoramiennymi. Jeśli bok kwadratu w podstawie ma długość 4 cm, a wysokość ostrosłupa wynosi 6 cm, to:

• Pp = 4 cm * 4 cm = 16 cm²
• Aby obliczyć Pb, potrzebujesz wysokości ściany bocznej. Załóżmy, że wynosi 5 cm. Pole jednej ściany bocznej = (4 cm * 5 cm)/2 = 10 cm². Mamy 4 ściany boczne, więc Pb = 4 * 10 cm² = 40 cm².
• Pc = 16 cm² + 40 cm² = 56 cm²
• V = (1/3) * 16 cm² * 6 cm = 32 cm³

Zapamiętaj te wzory i poćwicz na różnych przykładach, a sprawdzian z matematyki o ostrosłupach nie będzie Ci straszny! Pamiętaj o jednostkach! Pole powierzchni wyrażamy w jednostkach kwadratowych (np. cm²), a objętość w jednostkach sześciennych (np. cm³).