Sprawdzian Matematyka Trójkaty Prostokatne 2 Gim

Drodzy Nauczyciele Matematyki!

Zastanówmy się, jak skutecznie przygotować uczniów klasy drugiej gimnazjum do sprawdzianu z matematyki, a konkretnie z trójkątów prostokątnych. To ważny dział, który stanowi fundament dla dalszej nauki geometrii.

Kluczowe Zagadnienia

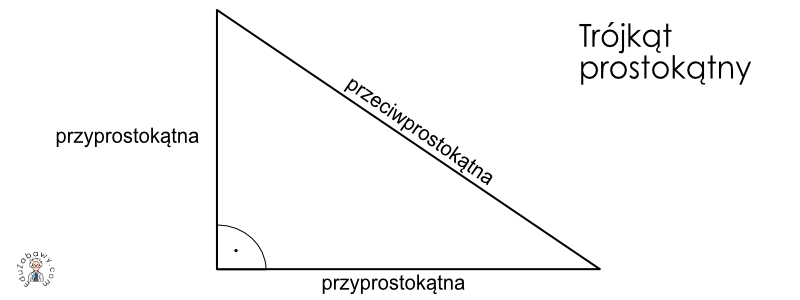
Przede wszystkim, solidne powtórzenie definicji. Trójkąt prostokątny musi być rozpoznawany bezbłędnie. Zwróćmy uwagę na kąt prosty i nazewnictwo boków: przeciwprostokątna (najdłuższy bok) oraz przyprostokątne.

Kolejny istotny element to twierdzenie Pitagorasa. a² + b² = c². Upewnijmy się, że uczniowie rozumieją, kiedy i jak je stosować. Nie tylko do obliczania długości boków, ale też do sprawdzania, czy trójkąt jest prostokątny.

Funkcje trygonometryczne sinus, cosinus i tangens kątów ostrych. Tu kluczowe jest zapamiętanie definicji w oparciu o stosunki boków w trójkącie prostokątnym. Przypomnijmy: sin α = przeciwległa/przeciwprostokątna, cos α = przyległa/przeciwprostokątna, tg α = przeciwległa/przyległa.

Typowe Błędy i Jak Ich Unikać

Powszechnym błędem jest mylenie boków przy stosowaniu twierdzenia Pitagorasa. Uczniowie często zapominają, który bok jest przeciwprostokątną. Wyraźnie to podkreślajmy!

Przy funkcjach trygonometrycznych problemy sprawia rozpoznanie boków przyległego i przeciwległego względem danego kąta. Pomocne mogą być ćwiczenia, w których uczniowie identyfikują te boki na różnych rysunkach.

Często spotykane są problemy z przekształcaniem wzorów, szczególnie przy obliczaniu długości przyprostokątnej, gdy znamy przeciwprostokątną i drugą przyprostokątną. Ćwiczenia z manipulacją wzorami są tu nieodzowne.

Jak Uatrakcyjnić Naukę?

Zastosujmy metody aktywizujące. Zamiast suchych definicji, użyjmy przykładów z życia codziennego. Drabina oparta o ścianę, przekątna prostokąta – to wszystko trójkąty prostokątne!

Wykorzystajmy gry i zabawy. Konkurs, kto szybciej obliczy długość boku trójkąta, może być świetną motywacją. Można też wykorzystać interaktywne narzędzia online.

Stwórzmy zadania problemowe. Uczniowie sami muszą znaleźć sposób na rozwiązanie problemu, wykorzystując wiedzę o trójkątach prostokątnych. To rozwija umiejętność logicznego myślenia.

Pamiętajmy o różnicowaniu poziomu trudności zadań. Dzięki temu każdy uczeń znajdzie coś dla siebie i będzie mógł odnieść sukces.

Podsumowanie

Gruntowne powtórzenie teorii, identyfikacja typowych błędów i zastosowanie metod aktywizujących to klucz do sukcesu uczniów na sprawdzianie z trójkątów prostokątnych. Powodzenia!