Sprawdzian Z Funkcji Trygonometrycznych 1 Liceum

Często na pierwszym roku liceum pojawia się sprawdzian z funkcji trygonometrycznych. Funkcje trygonometryczne to kluczowy element matematyki. Przygotowanie do niego wymaga zrozumienia kilku podstawowych pojęć i umiejętności.
Definicje Podstawowych Funkcji Trygonometrycznych
Zacznijmy od definicji. Mamy trzy podstawowe funkcje: sinus (sin), cosinus (cos), i tangens (tg). Rozpatrujemy je w kontekście trójkąta prostokątnego. Sinus kąta to stosunek długości przyprostokątnej przeciwległej do kąta, do długości przeciwprostokątnej. Cosinus kąta to stosunek długości przyprostokątnej przyległej do kąta, do długości przeciwprostokątnej. Tangens kąta to stosunek długości przyprostokątnej przeciwległej do kąta, do długości przyprostokątnej przyległej.
Możemy to zapisać wzorami:
- sin(α) = a/c
- cos(α) = b/c
- tg(α) = a/b
Wartości Funkcji Trygonometrycznych dla Kątów Charakterystycznych
Istnieją kąty, dla których warto znać wartości funkcji trygonometrycznych na pamięć. Są to kąty: 0°, 30°, 45°, 60° i 90°. Ułatwia to rozwiązywanie wielu zadań. Można stworzyć tabelkę, która pomoże w zapamiętaniu tych wartości.
Na przykład:
- sin(30°) = 1/2
- cos(60°) = 1/2
- tg(45°) = 1
Tożsamości Trygonometryczne
Tożsamości trygonometryczne to równania, które są prawdziwe dla wszystkich wartości kątów. Są one bardzo przydatne przy upraszczaniu wyrażeń trygonometrycznych. Najważniejszą tożsamością jest jedynka trygonometryczna: sin²(α) + cos²(α) = 1.
Inne ważne tożsamości to:
- tg(α) = sin(α)/cos(α)
- ctg(α) = cos(α)/sin(α)
Zastosowanie Funkcji Trygonometrycznych
Funkcje trygonometryczne mają szerokie zastosowanie w różnych dziedzinach. Używane są w fizyce do opisu ruchu falowego. Stosuje się je w geodezji do pomiarów odległości i kątów. Wykorzystywane są również w nawigacji.
Przykład: obliczanie wysokości drzewa, znając kąt pod jakim widzimy jego wierzchołek i odległość od drzewa. Możemy użyć funkcji tangens, aby obliczyć wysokość drzewa.
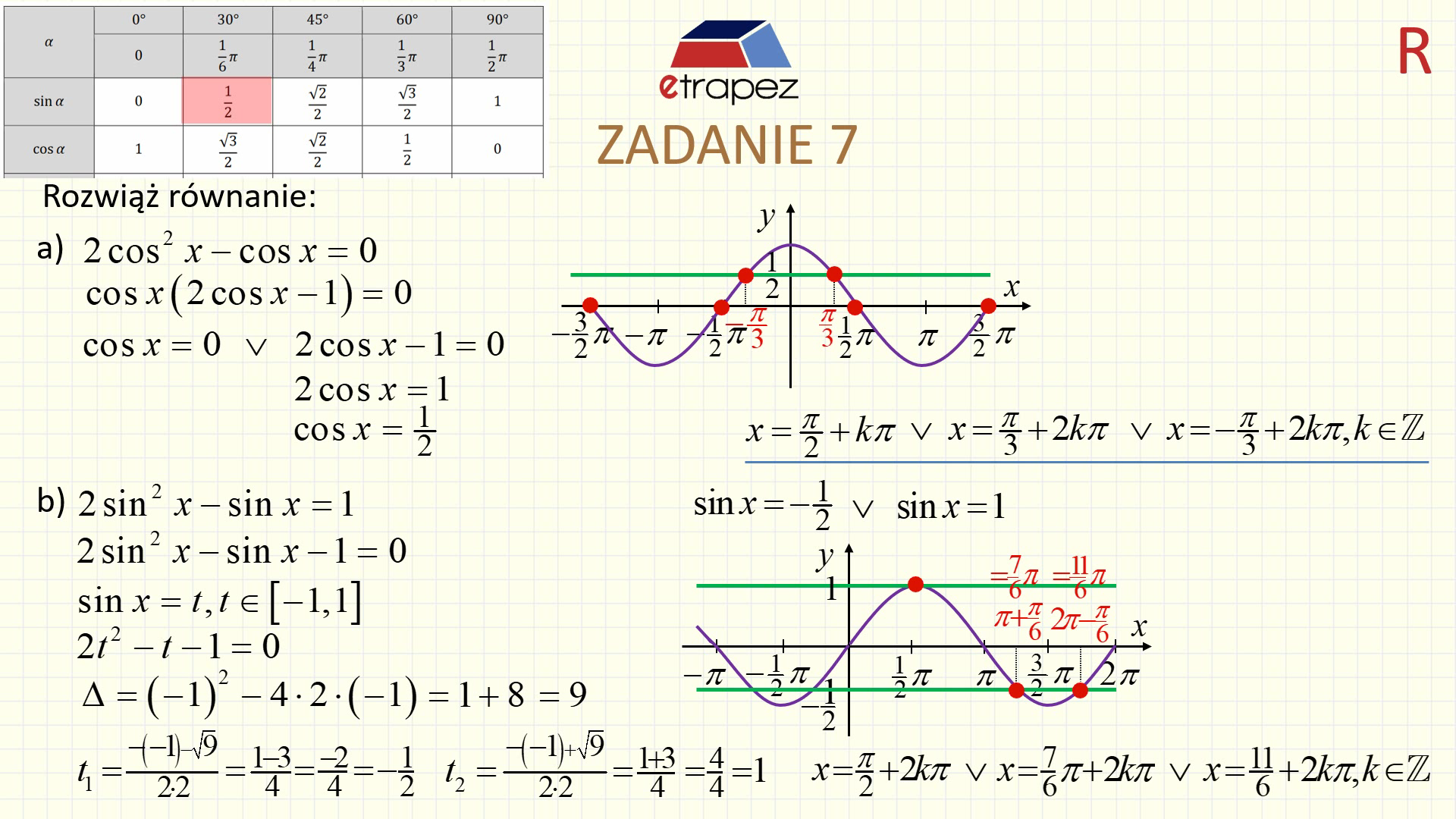
Równania Trygonometryczne
Równania trygonometryczne to równania, w których niewiadoma występuje jako argument funkcji trygonometrycznej. Rozwiązywanie takich równań polega na znalezieniu wszystkich kątów, które spełniają dane równanie. Należy pamiętać o okresowości funkcji trygonometrycznych. Oznacza to, że istnieje nieskończenie wiele rozwiązań.
Na przykład, rozwiązaniem równania sin(x) = 1/2 są kąty x = 30° + k * 360° oraz x = 150° + k * 360°, gdzie k jest liczbą całkowitą.
Pamiętaj, że solidne zrozumienie definicji, wartości funkcji dla kątów charakterystycznych, tożsamości i umiejętność rozwiązywania prostych równań trygonometrycznych to klucz do sukcesu na sprawdzianie z funkcji trygonometrycznych.