Sprawdzian Z Funkcji Trygonometrycznych 2 Liceum

Sprawdzian Z Funkcji Trygonometrycznych 2 Liceum to test sprawdzający wiedzę z zakresu funkcji trygonometrycznych, przeprowadzany zazwyczaj w drugiej klasie liceum. Obejmuje zagadnienia takie jak sinus, cosinus, tangens, cotangens, ich definicje, wykresy, własności oraz zastosowania.
Aby dobrze przygotować się do sprawdzianu, wykonajmy kilka kroków:
Krok 1: Definicje Funkcji Trygonometrycznych. Musisz znać definicje sinusa, cosinusa, tangensa i cotangensa w trójkącie prostokątnym (stosunek boków) oraz na okręgu jednostkowym. Na przykład, w trójkącie prostokątnym, sinus kąta α to stosunek długości boku przeciwległego do kąta α do długości przeciwprostokątnej.
Przykład: Jeżeli bok przeciwległy kątowi α ma długość 3, a przeciwprostokątna ma długość 5, to sin(α) = 3/5.
Krok 2: Wykresy Funkcji. Naucz się rysować i interpretować wykresy funkcji sinus, cosinus, tangens i cotangens. Zwróć uwagę na okres, amplitudę, przesunięcia, asymptoty (dla tangensa i cotangensa) oraz punkty charakterystyczne (np. miejsca zerowe, ekstrema).
Przykład: Wykres funkcji sinus zaczyna się w punkcie (0,0), a jego okres wynosi 2π.
Krok 3: Wzory i Tożsamości. Opanuj wzory trygonometryczne, takie jak jedynka trygonometryczna (sin2α + cos2α = 1), wzory redukcyjne, wzory na sumę i różnicę kątów, podwojony kąt, itp.
Przykład: Aby obliczyć sin(2α), użyj wzoru sin(2α) = 2sin(α)cos(α).
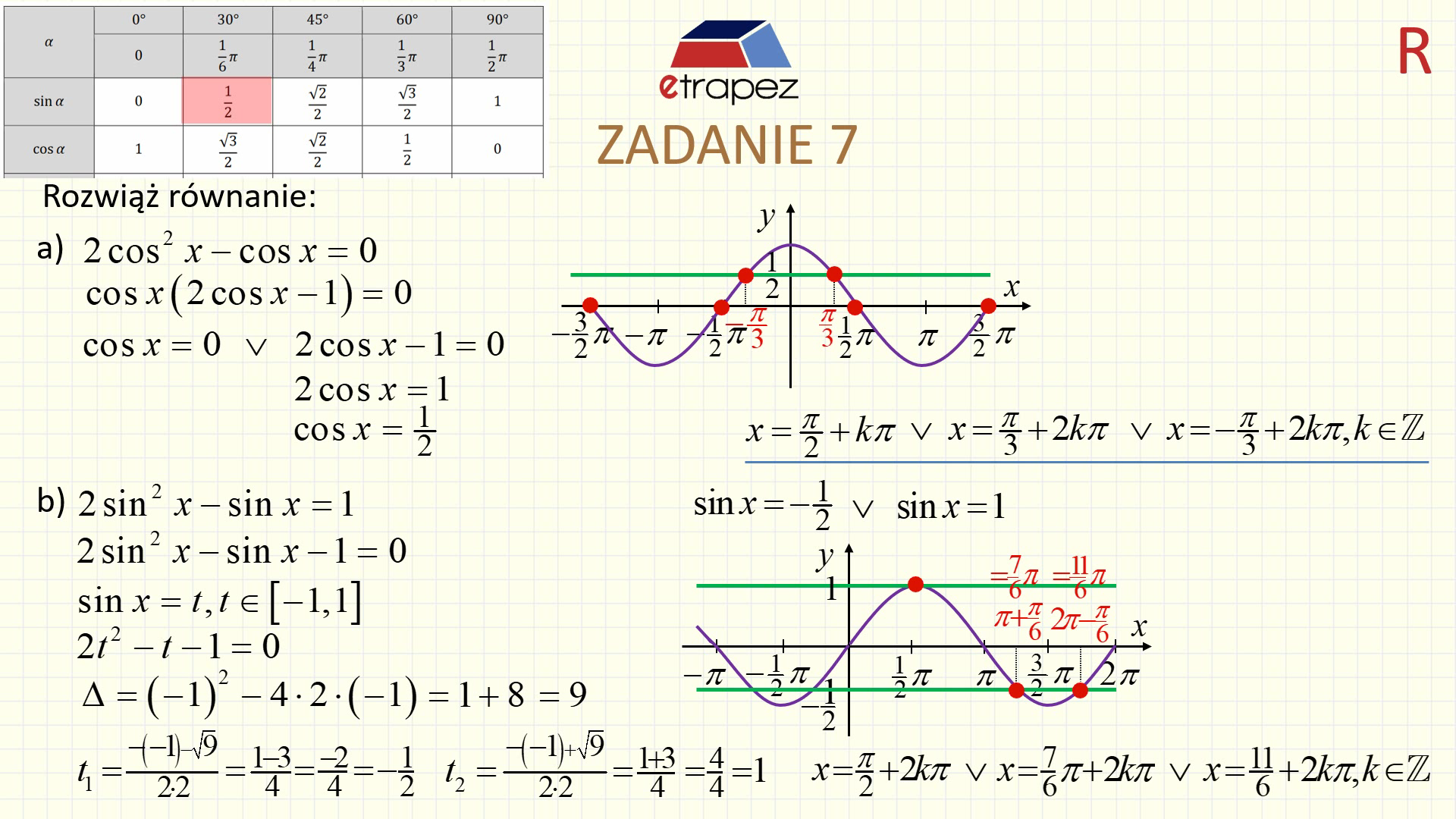
Krok 4: Rozwiązywanie Równań Trygonometrycznych. Ćwicz rozwiązywanie równań trygonometrycznych, zarówno prostych, jak i bardziej złożonych. Pamiętaj o uwzględnianiu okresowości funkcji i wyznaczaniu wszystkich rozwiązań w danym przedziale.
Przykład: Rozwiązując równanie sin(x) = 1/2, otrzymujesz x = π/6 + 2kπ lub x = 5π/6 + 2kπ, gdzie k jest liczbą całkowitą.
Funkcje trygonometryczne są bardzo ważne, na przykład w fizyce do opisywania ruchów harmonicznych (np. wahadło) oraz w nawigacji, gdzie wykorzystuje się je do określania pozycji na podstawie kątów.