Sprawdzian Z Matematyki 1 Liceum Wykresy Funkcji

Sprawdzian z matematyki w 1 liceum często obejmuje wykresy funkcji. Ale czym tak naprawdę jest wykres funkcji?

Co to jest Wykres Funkcji?

Najprościej mówiąc, wykres funkcji to obrazek. Ten obrazek pokazuje, jak zmienia się wartość funkcji (zwykle oznaczana jako y) w zależności od wartości argumentu (zwykle oznaczanego jako x). Pomyśl o tym jak o mapie, która pokazuje związek pomiędzy dwoma rzeczami.

Krok po Kroku: Jak to Działa?

Funkcja: Najpierw potrzebujesz funkcji. Funkcja to przepis, który mówi, co zrobić z liczbą x, żeby dostać liczbę y. Na przykład: y = x + 2.
Argument (x): To liczba, którą wstawiasz do funkcji. Możesz wybrać dowolną liczbę.
Wartość Funkcji (y): To wynik, który otrzymujesz po wstawieniu x do funkcji. W naszym przykładzie, jeśli x = 1, to y = 1 + 2 = 3.
Punkt: Każdą parę (x, y) możesz zaznaczyć jako punkt na układzie współrzędnych. Układ współrzędnych to po prostu dwie linie: pozioma (oś x) i pionowa (oś y).
Wykres: Zaznaczając wiele punktów (x, y) i łącząc je linią, otrzymasz wykres funkcji.

Przykłady i Interpretacja

Wyobraź sobie funkcję, która opisuje wysokość rzuconej piłki (y) w zależności od czasu (x). Na początku, piłka jest nisko, potem leci w górę, osiąga szczyt, a następnie spada. Wykres funkcji pokaże tę trajektorię – będzie to krzywa w kształcie paraboli.

Inny przykład: funkcja opisująca temperaturę (y) w ciągu dnia (x). Rano temperatura jest niska, potem rośnie w ciągu dnia, a wieczorem spada. Wykres pokaże linię, która najpierw idzie w górę, a potem w dół.

Dlaczego Wykresy Są Ważne?

Wykresy funkcji pomagają zrozumieć, jak zmienia się coś w zależności od czegoś innego. Pozwalają zobaczyć trendy i zależności, które trudno byłoby zauważyć, patrząc tylko na liczby.

Czego Szukać na Sprawdzianie?

Na sprawdzianie możesz spotkać się z różnymi zadaniami związanymi z wykresami funkcji:

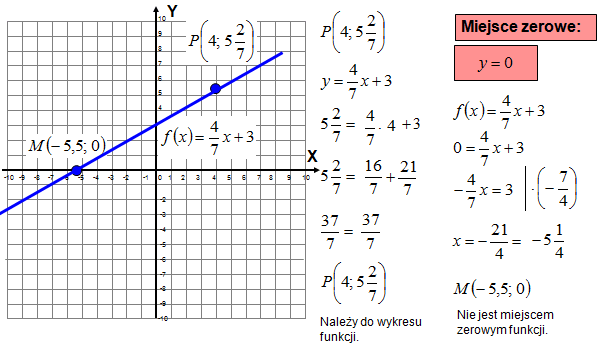
Rysowanie wykresu na podstawie wzoru funkcji.
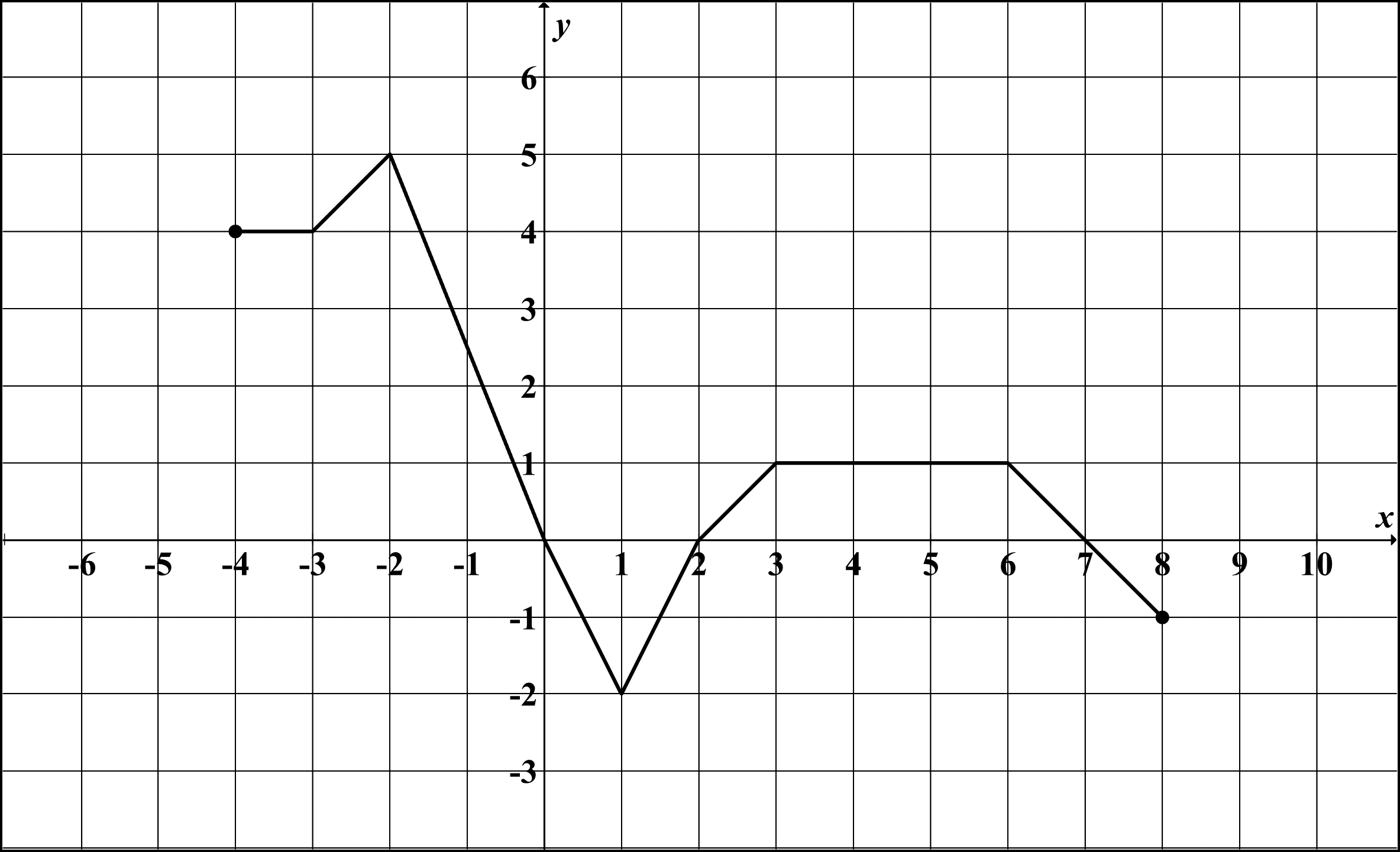
Odczytywanie informacji z wykresu (np. jakie wartości przyjmuje funkcja dla konkretnych x).
Określanie własności funkcji na podstawie wykresu (np. gdzie funkcja rośnie, a gdzie maleje).
Dopasowywanie wzoru funkcji do danego wykresu.

Pamiętaj, że kluczem do sukcesu jest praktyka. Rozwiązuj zadania i analizuj różne wykresy funkcji. Im więcej ćwiczysz, tym łatwiej zrozumiesz, jak działają i jakie informacje można z nich wyczytać. Powodzenia!