Sprawdzian Z Trójkątów Prostokątnych 2 Gimnazjum

Sprawdzian z Trójkątów Prostokątnych 2 Gimnazjum – to po prostu test sprawdzający Twoją wiedzę o trójkątach prostokątnych, a konkretnie w szkole podstawowej (gimnazjum już nie istnieje, ale termin pozostał). Skupia się na umiejętności rozwiązywania zadań z wykorzystaniem Twierdzenia Pitagorasa, funkcji trygonometrycznych i własności kątów w takim trójkącie.

Co musisz wiedzieć?

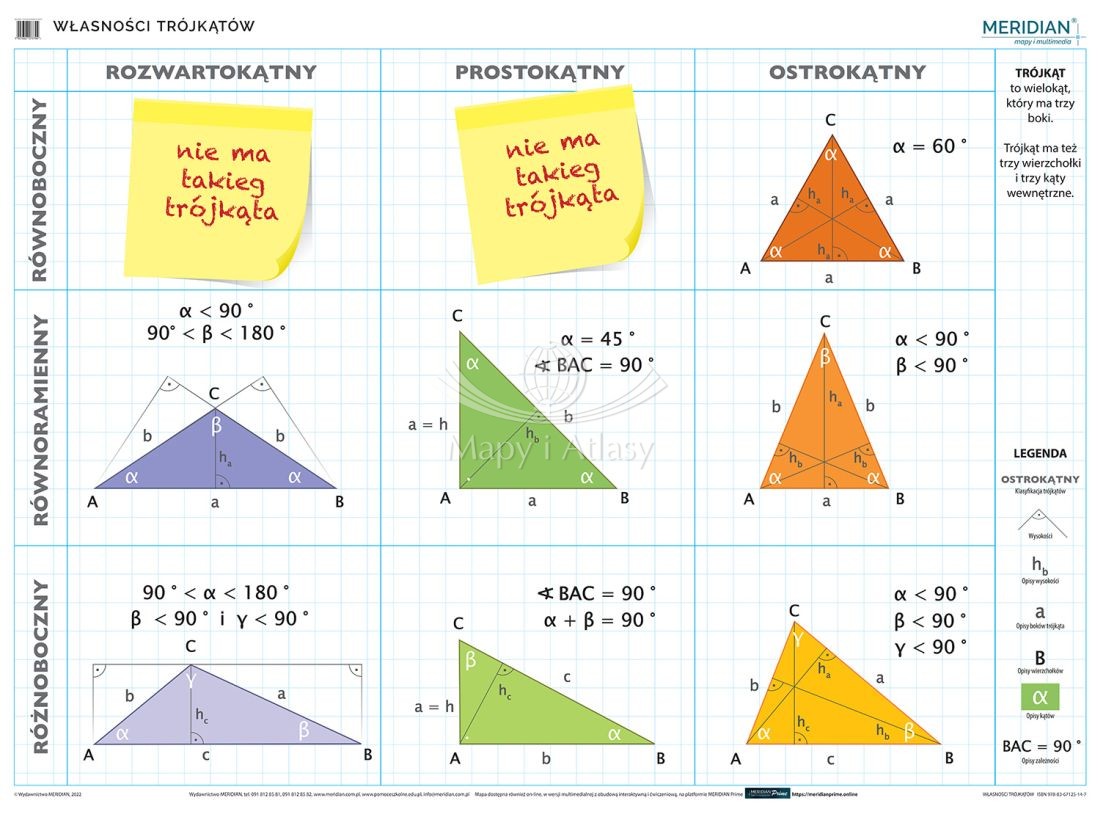
Trójkąt prostokątny to trójkąt, w którym jeden z kątów jest kątem prostym (90 stopni). Bok naprzeciwko kąta prostego to przeciwprostokątna – najdłuższy bok w trójkącie. Pozostałe dwa boki to przyprostokątne.

Twierdzenie Pitagorasa jest kluczowe: a² + b² = c². Gdzie a i b to długości przyprostokątnych, a c to długość przeciwprostokątnej. Używamy go, aby obliczyć długość jednego z boków, gdy znamy długości dwóch pozostałych.

Przykład: Jeśli przyprostokątne mają długości 3 i 4, to przeciwprostokątna ma długość 5, ponieważ 3² + 4² = 9 + 16 = 25, a pierwiastek z 25 to 5.

Funkcje Trygonometryczne

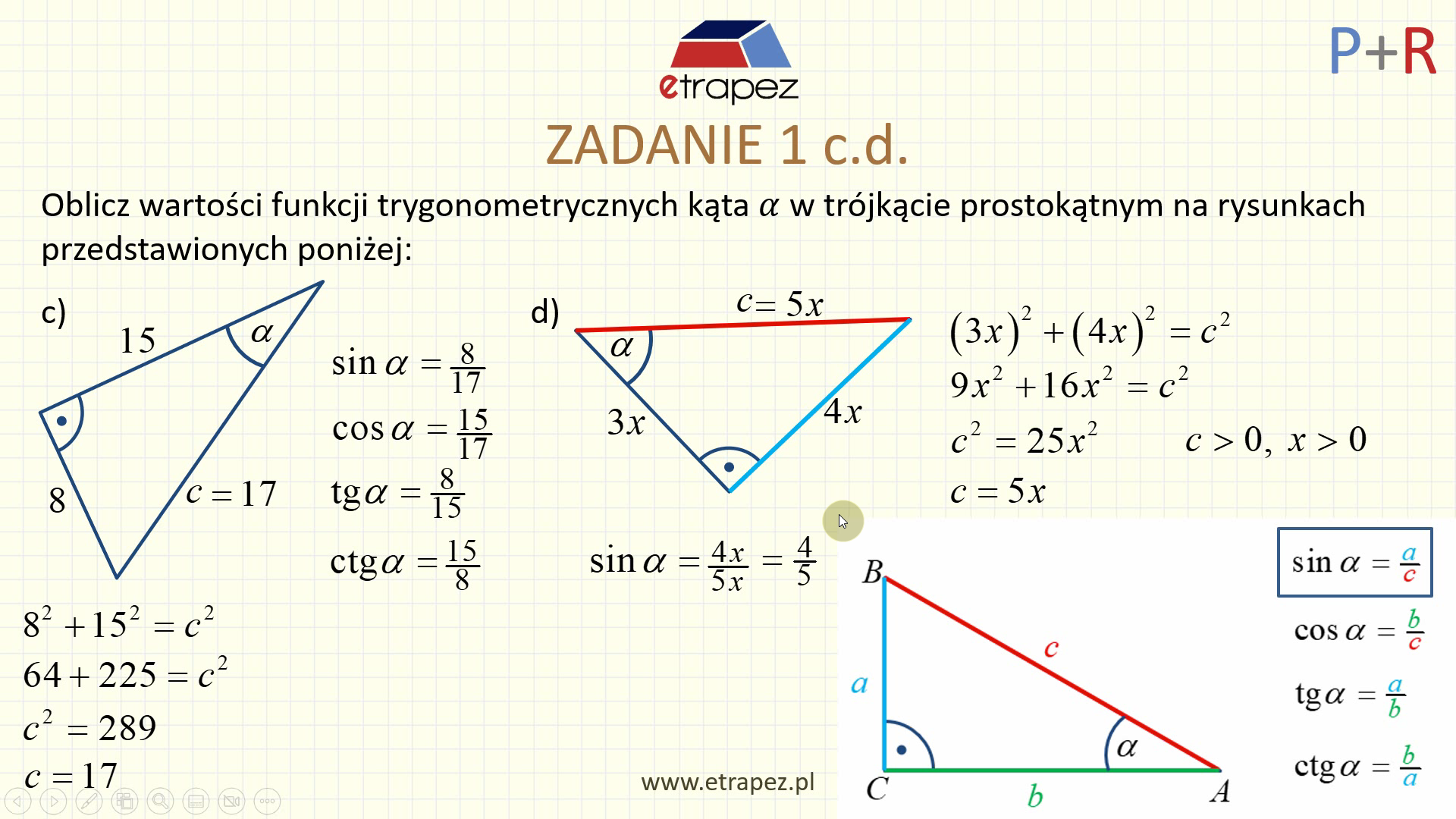
Dla kątów ostrych w trójkącie prostokątnym definiujemy funkcje trygonometryczne: sinus (sin), cosinus (cos) i tangens (tg).

Sinus kąta to stosunek długości przyprostokątnej naprzeciwległej do tego kąta do długości przeciwprostokątnej.
Cosinus kąta to stosunek długości przyprostokątnej przyległej do tego kąta do długości przeciwprostokątnej.
Tangens kąta to stosunek długości przyprostokątnej naprzeciwległej do długości przyprostokątnej przyległej.

Można to zapamiętać jako SOH CAH TOA: * SOH: Sin = Opposite / Hypotenuse * CAH: Cos = Adjacent / Hypotenuse * TOA: Tan = Opposite / Adjacent

Przykład: Masz trójkąt prostokątny, gdzie kąt α wynosi 30 stopni, a przeciwprostokątna ma długość 10. Chcesz obliczyć długość przyprostokątnej naprzeciwległej kątowi α. Użyjesz sinusa: sin(30°) = (przyprostokątna naprzeciwległa) / 10. Wiemy, że sin(30°) = 0.5. Zatem przyprostokątna naprzeciwległa = 0.5 * 10 = 5.

Kąty w Trójkącie Prostokątnym

Suma kątów w każdym trójkącie wynosi 180 stopni. W trójkącie prostokątnym jeden kąt ma 90 stopni, więc suma dwóch pozostałych kątów musi wynosić 90 stopni. Te dwa kąty nazywamy kątami ostrymi.

Przykład: Jeśli jeden kąt ostry ma 60 stopni, to drugi kąt ostry ma 30 stopni (90 - 60 = 30).

Na co zwrócić uwagę na sprawdzianie?

Sprawdzian może zawierać zadania, w których trzeba:

Obliczyć długość boku trójkąta prostokątnego z Twierdzenia Pitagorasa.
Wykorzystać funkcje trygonometryczne do obliczenia długości boków lub miar kątów.
Rozwiązywać zadania tekstowe dotyczące trójkątów prostokątnych (np. wysokość drzewa, odległość między punktami).

Pamiętaj o jednostkach! Upewnij się, że podajesz odpowiednie jednostki długości (np. cm, m) i kątów (np. stopnie).

Powodzenia na sprawdzianie!