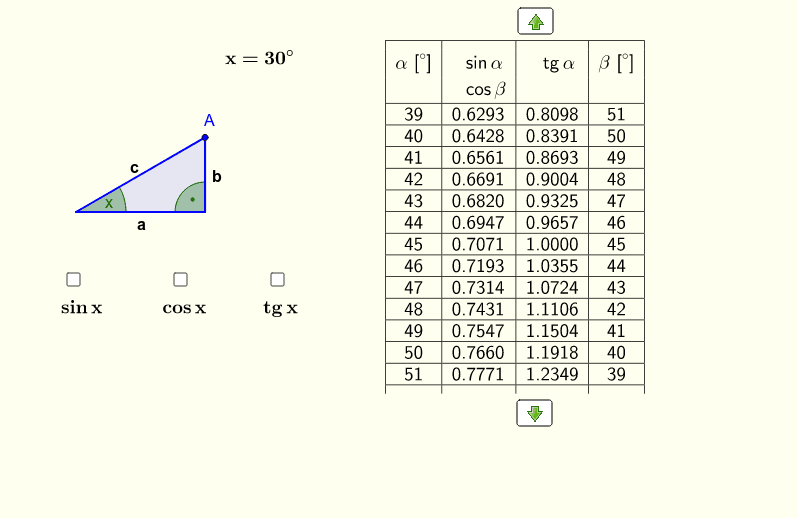
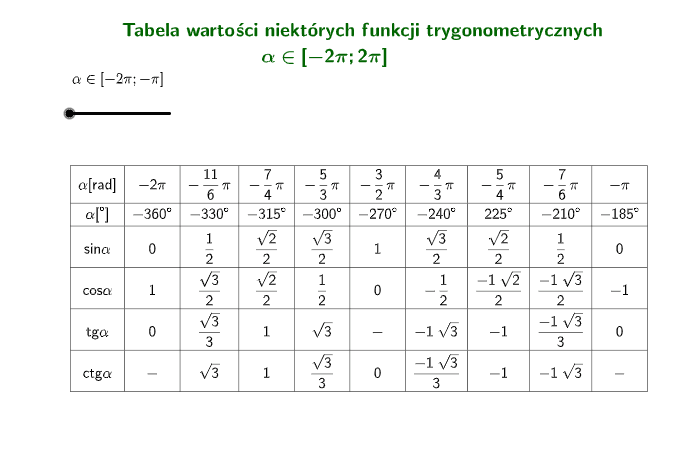
Wartości Funkcji Trygonometrycznych Kątów Ostrych

Wartości funkcji trygonometrycznych kątów ostrych to liczby, które opisują proporcje boków w trójkącie prostokątnym. Mówią nam, jaki jest związek między kątem ostrym a długościami jego boków.

Czym jest trójkąt prostokątny?

Trójkąt prostokątny to trójkąt, który ma jeden kąt prosty (90 stopni). Najdłuższy bok, leżący naprzeciwko kąta prostego, nazywamy przeciwprostokątną. Pozostałe dwa boki to przyprostokątne.

Funkcje trygonometryczne: sinus, cosinus i tangens

Dla kąta ostrego (mniejszego niż 90 stopni) w trójkącie prostokątnym, definiujemy trzy podstawowe funkcje trygonometryczne:

• Sinus (sin): to stosunek długości przyprostokątnej naprzeciwległej do kąta do długości przeciwprostokątnej. Czyli: sin(kąt) = (długość przyprostokątnej naprzeciwległej) / (długość przeciwprostokątnej).
• Cosinus (cos): to stosunek długości przyprostokątnej przyległej do kąta do długości przeciwprostokątnej. Czyli: cos(kąt) = (długość przyprostokątnej przyległej) / (długość przeciwprostokątnej).
• Tangens (tan): to stosunek długości przyprostokątnej naprzeciwległej do kąta do długości przyprostokątnej przyległej do kąta. Czyli: tan(kąt) = (długość przyprostokątnej naprzeciwległej) / (długość przyprostokątnej przyległej).

Przykład

Wyobraźmy sobie trójkąt prostokątny. Kąt ostry, którym się zajmujemy, ma miarę 30 stopni. Załóżmy, że przyprostokątna naprzeciwległa ma długość 5, a przeciwprostokątna ma długość 10.

• sin(30°) = 5/10 = 0.5

Wiemy, że cosinus 30° wynosi około 0.866. Zakładając, że znamy długość przeciwprostokątnej (10), możemy obliczyć długość przyprostokątnej przyległej: cos(30°) = (długość przyprostokątnej przyległej) / 10. Zatem, długość przyprostokątnej przyległej wynosi około 8.66.

Tangens 30° wynosi około 0.577. Możemy to obliczyć, dzieląc długość przyprostokątnej naprzeciwległej (5) przez długość przyprostokątnej przyległej (8.66): tan(30°) = 5 / 8.66 ≈ 0.577.

Znaczenie wartości funkcji trygonometrycznych

Wartości funkcji trygonometrycznych są bardzo ważne w wielu dziedzinach, takich jak fizyka, inżynieria i nawigacja. Pozwalają na obliczanie odległości, kątów nachylenia i wiele innych parametrów, korzystając jedynie z miary kąta i długości jednego boku w trójkącie prostokątnym. Na przykład, pomagają określić wysokość budynku, znając kąt, pod jakim go widzimy z pewnej odległości, i odległość od tego budynku.

Podsumowanie

Funkcje trygonometryczne, takie jak sinus, cosinus i tangens, opisują relacje między kątami ostrymi a bokami w trójkącie prostokątnym. Są one podstawowym narzędziem w rozwiązywaniu problemów geometrycznych i znajdują zastosowanie w wielu dziedzinach nauki i techniki. Zrozumienie definicji tych funkcji i sposobów ich obliczania jest kluczowe dla dalszej nauki matematyki i jej zastosowań.